학습목표
- 스택 자료구조의 개념과 동작 방식을 이해한다.
- 배열 스택과 연결리스트 스택을 구현할 수 있다.
- 자바 Stack 클래스를 활용할 수 있다
- 괄호쌍 체크, 중위식을 후위식 변환, 후위식 계산 등 스택 응용을 구현할 수 있다.
1. 스택 개념
스택(Stack)은 ‘더미’ 또는 ‘쌓아 올림’을 의미하는 용어로, 데이터를 쌓아 올리는 형태로 저장하고 있어, 데이터를 추출할 때는 맨 위에 있는 데이터를 먼저 꺼내는 형태이다. 따라서, 스택은 제일 마지막에 저장한 데이터를 제일 먼저 꺼내는 후입선출(LIFO, Last In First Out) 형태의 자료 구조이다.
스택은 가장 마지막 데이터의 위치인 top에서 삽입이나 삭제가 발생하므로 구조적으로 한 쪽 방향에서만 입출력이 수행된다.
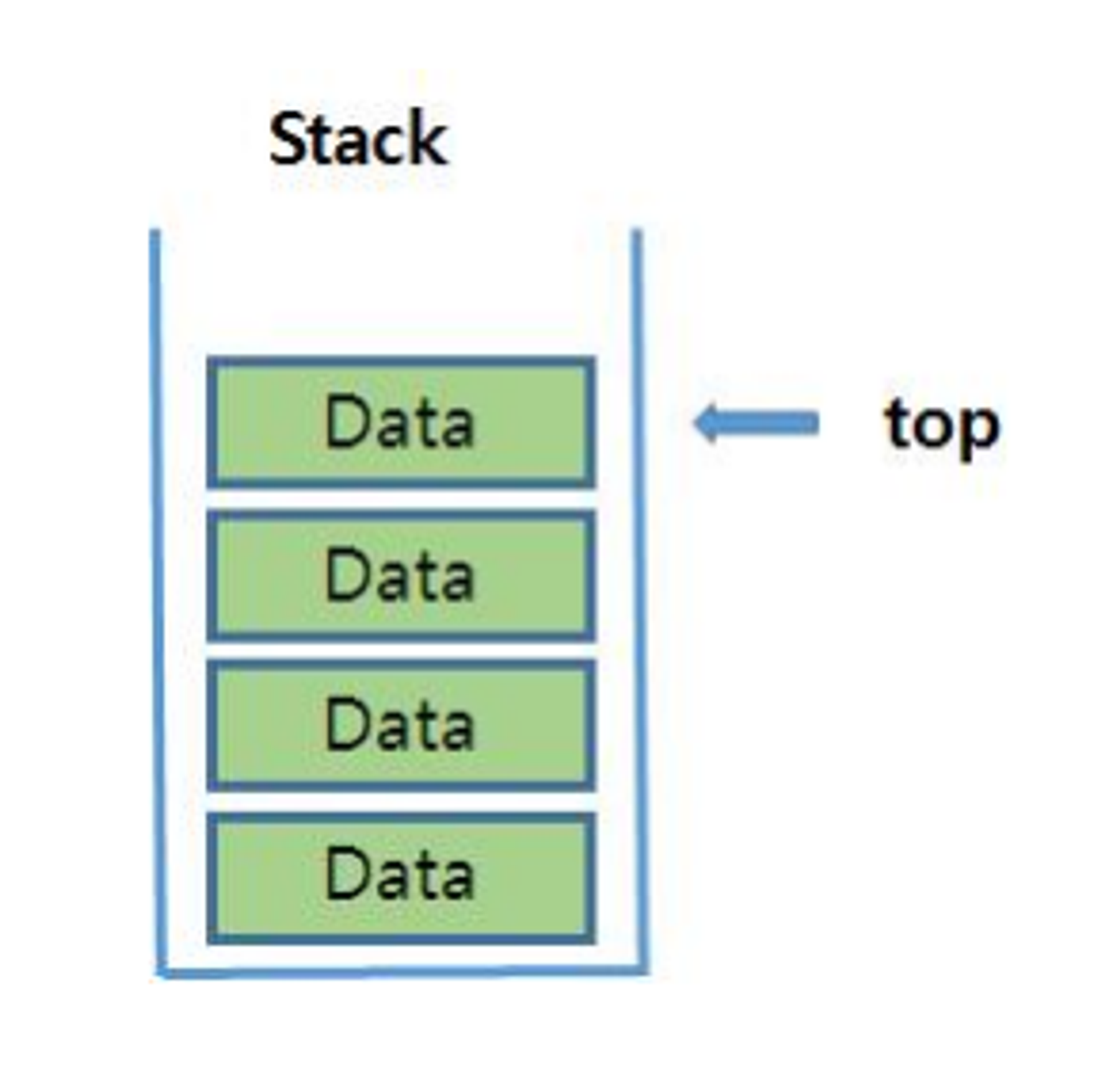
스택의 동작(연산)
- 삽입 연산 : push
- 삭제(추출) 연산 : pop
- 읽기 연산 : peek
2. 스택 구현
배열을 이용한 구현(배열 스택)
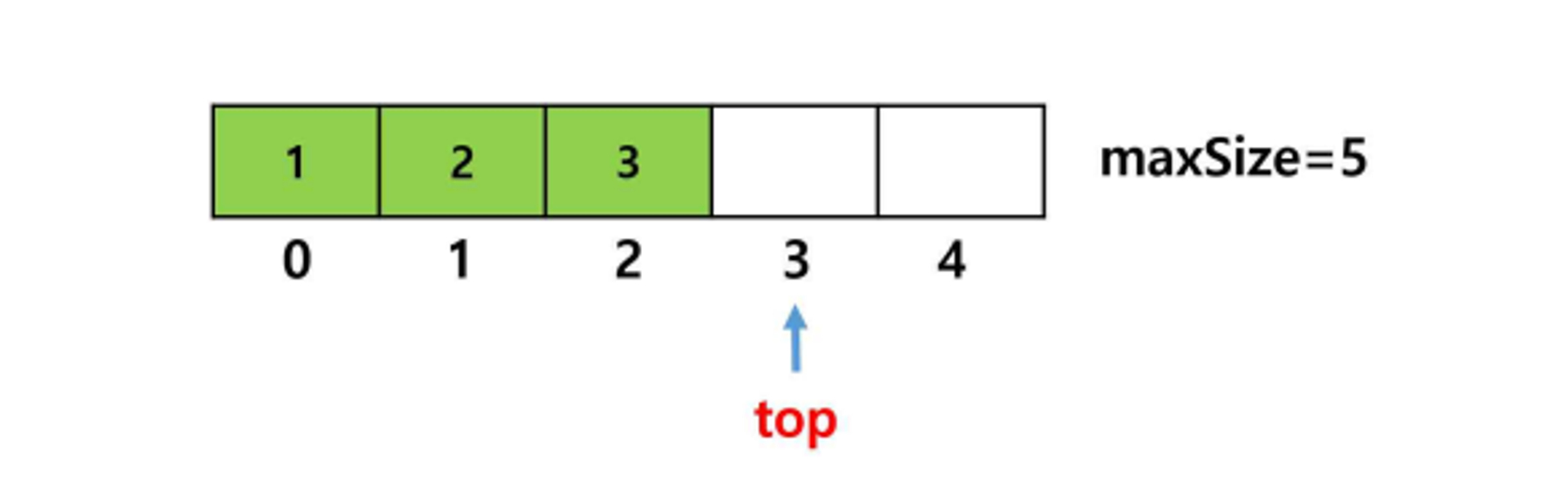
- 배열이 꽉 찼는지 체크를 무조건 해줘야 한다. → overflow 발생
package s240326;
class ArrayStack {
private Integer data[];
private int top;
private int maxSize;
public ArrayStack(int initsize) { // 생성자
data = new Integer[initsize];
top = 0;
maxSize = initsize;
}
public boolean empty() { // 공백 상태 체크
return top == 0;
}
public boolean full() { // 포화상태 체크
return top == maxSize;
}
public void push(Integer elem) { // push 연산
if (top == maxSize){
System.out.println("overflow"); // 스택이 꽉차면 overflow
return;
}
data[top++] = elem;
}
public Integer pop() { // pop 연산
if (top > 0)
return data[--top];
else
return null; // 스택이 비어있으면 null 반환
}
}
public class ArrayStackTest {
public static void main(String[] args) {
ArrayStack as = new ArrayStack(5); // 크기가 5인 배열 스택 생성
for (int i = 1; i <= 5; i++)
as.push(i); // 스택에 push
System.out.print("Pop : ");
for (int i = 1; i <= 5; i++)
System.out.print(as.pop()+" "); // 스택에서 pop(역순출력)
}
}
연결 리스트를 이용한 구현(연결 스택)
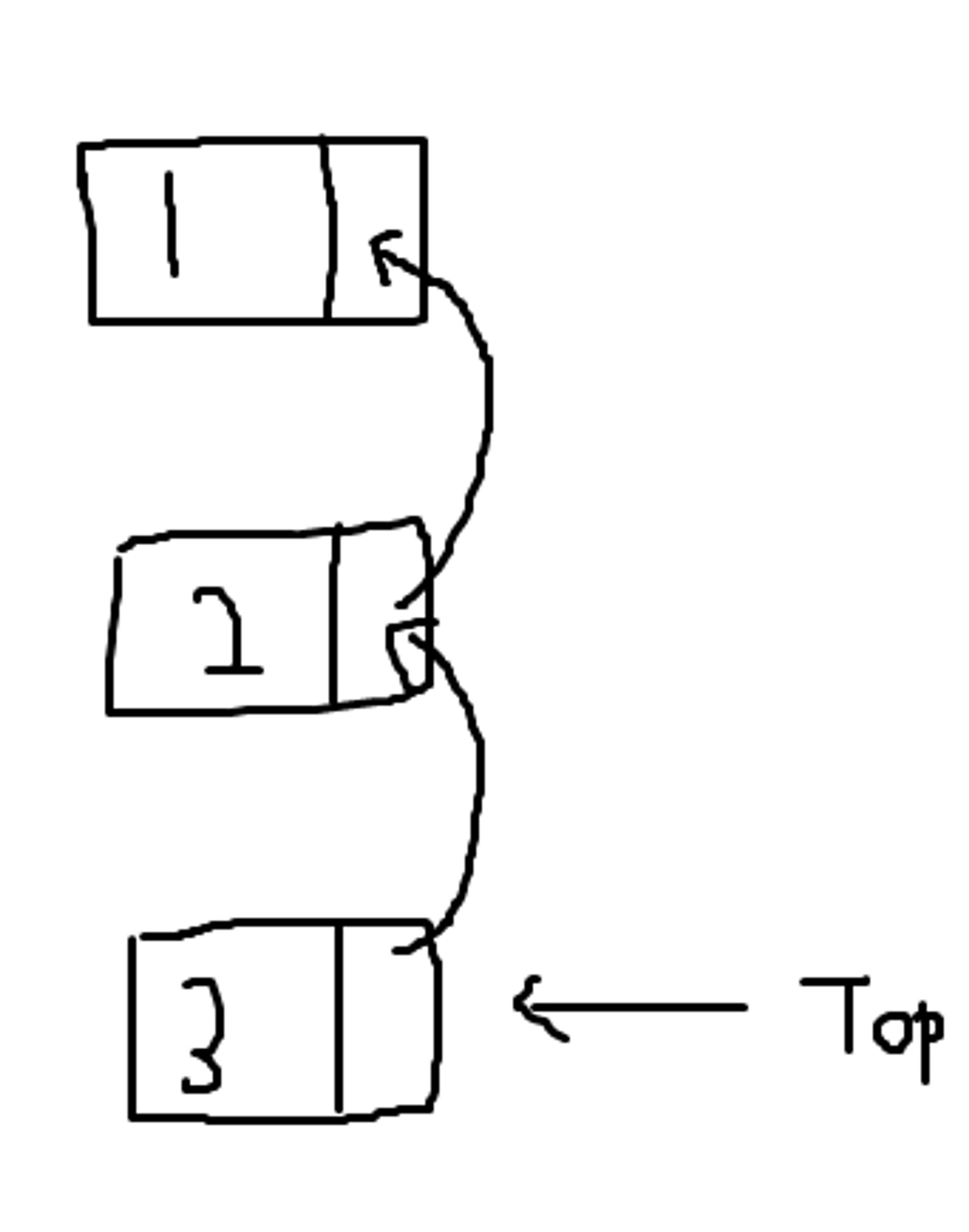
1 , 2 , 3 이라는 데이터를 순서대로 넣었을 때 내부에는 해당 형태로 생성되게 된다. 가장 나중에 들어간 것에 Top 포인터가 가르키고 있다.
package s240326;
class LinkedStack {
private Node top;
// 노드 class 단순연결 리스트와 같다.
private class Node{
private Integer data;
private Node nextNode;
Node(Integer data){
this.data = data;
this.nextNode = null;
}
}
// 생성자, stack이 비어있으므로 top은 null이다.
public LinkedStack(){
this.top = null;
}
// 스택이 비어있는지 확인
public boolean empty(){
return (top == null);
}
// item을 스택의 top에 넣는다.
public void push(Integer item){Node newNode = new Node(item);
newNode.nextNode = top;
top = newNode;
}
// top 노드의 데이터를 반환한다.
public Integer peek(){
if(empty()) {
System.out.println("공백상태");
return null;
}
return top.data;
}
// top 노드를 스택에서 제거한다.
public Integer pop(){
Integer item = peek();
top = top.nextNode;
return item;
}
}
public class LinkedStackTest {
public static void main(String[] args) {
LinkedStack s = new LinkedStack(); // 연결 스택 생성
for (int i = 1; i <= 5; i++)
s.push(i);
System.out.print("Pop : ");
for (int i = 1; i <= 5; i++)
System.out.print(s.pop() + " ");
}
}
자바 Stack 활용
- Stack<Integer> st = new Stack<>(); - 스택에 정수 객체를 저장할 경우
- Stack<String> st = new Stack<>(); - 스택에 String 객체를 저장할 경우
자바 Stack 클래스의 주요 메소드들은 다음과 같다
- E push(E item) : 스택의 top 위치에 item을 입력한다.
- E pop() : 스택의 top 위치에서 데이터를 추출(삭제)하여 반환한다.
- E peek() : 스택의 top 위치에서 데이터를 읽어서 반환한다. 삭제는 하지 않는다.
- boolean empty() : 스택이 비워있는지 여부를 반환한다. 빈 스택이면 true 반환.
자바 Stack 클래스는 내부적으로 연결리스트를 사용하여 구현되어 있어서 스택이 가득 차 있는지를 별도로 확인할 필요가 없다.
스택 응용
스택은 입력 데이터를 역순으로 출력하고자 하는 곳에는 모두 사용 가능한 자료구조이다.
- 수식의 괄호 검사(괄호 쌍 검사)
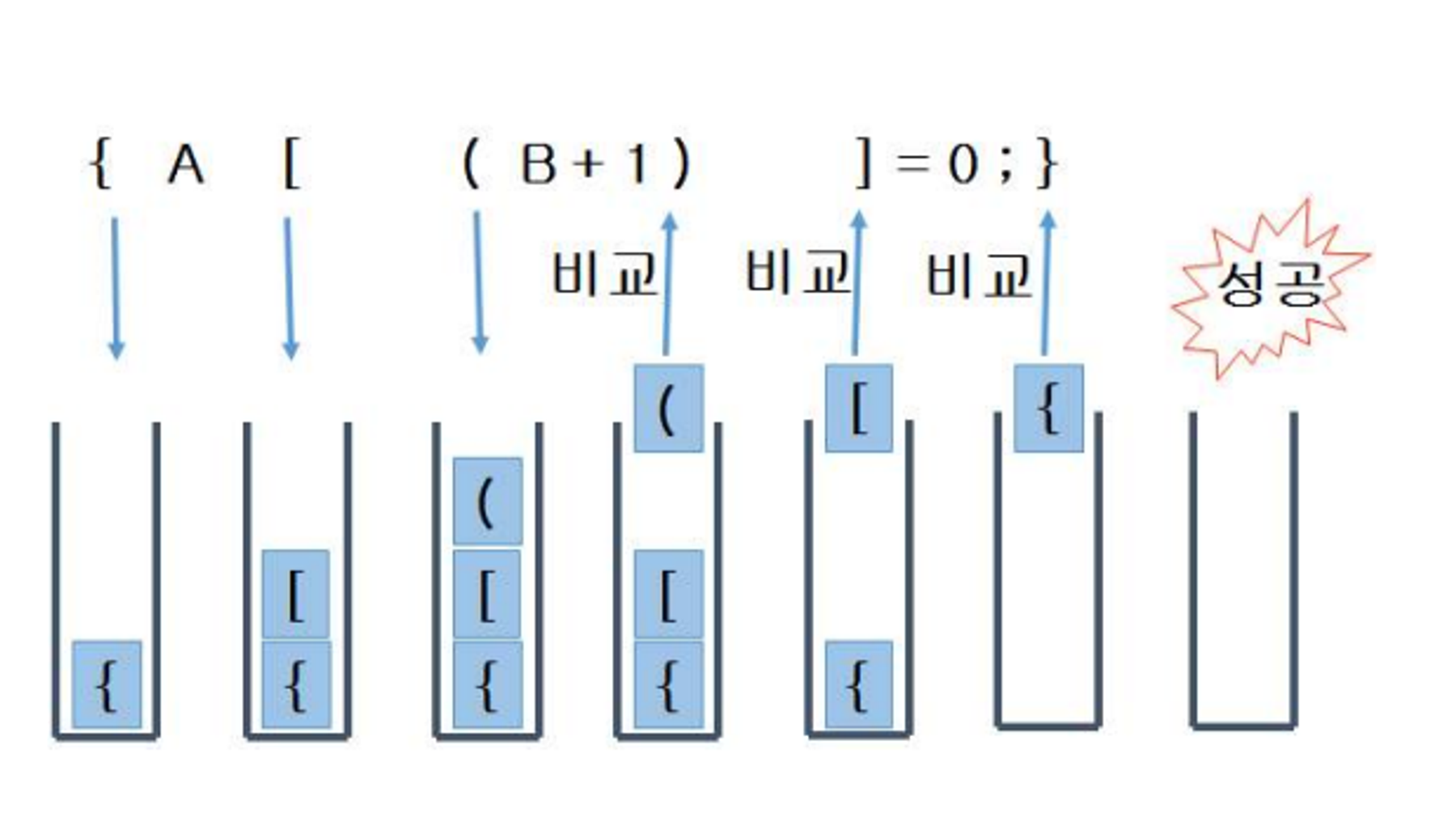
가장 마지막에 연 괄호를 제일 먼저 닫아 줘야하는데 우리가 생각할 수 있는 후입선출의 로직으로 pop 연산을 이용하여 꺼내면 가장 마지막에 입력된 괄호부터 pop이 되게 된다.

괄호 쌍을 체크하는 알고리즘
- 입력 : 괄호 포함 수식
- 결과 : 괄호 쌍이 맞으면 true, 실패 시 false 반환
package s240326;
import java.util.Stack;
class Formula {
private String exp;
private int expSize;
private char testCh, openPair;
public boolean checkMatching(String exp){ // 괄호쌍 체크 메소드 : 올바르면 true 반환
this.exp = exp;
Stack<Character> stack = new Stack<>(); // 문자형객체 Stack 생성
expSize = this.exp.length();
for(int i=0; i<expSize; i++){
testCh = exp.charAt(i);
switch(testCh){ // 여는 괄호면 스택에 푸시
case '(' :
case '[' :
case '{' :
stack.push(testCh); // 오토박싱, char 기초형이 Character 객체로 변환되어 저장
break;
case ')' : // 닫는 괄호면 스택에서 팝 후, 괄호쌍 매칭 검사
case ']' :
case '}' :
if(stack.empty()){
return false;
}else{
openPair = stack.pop();
if( openPair=='(' && testCh!=')' ||
openPair=='{' && testCh!='}' ||
openPair=='[' && testCh!=']' ) {
return false;
} else {
break;
}
}
}
}
if(stack.empty()) // 수식을 모두 읽은 후, 스택이 비어 있으면 오케이
return true;
else
return false;
}
}
public class FormulaTest {
public static void main(String[] args) {
Formula op = new Formula();
String exp = "{(A+B)-3}*5+[{cos(x+y)+7}-1]*4";
System.out.println(exp);
if(op.checkMatching(exp))
System.out.println("수식이 올바름(괄호의 쌍이 일치)");
else
System.out.println("수식이 올바르지 않음(괄호의 쌍이 불일치)");
}
}
- 후위식 계산
수식의 표기법에는 연산자의 위치에 따라 전위, 후위, 중위 표기법으로 나누어진다.
전위 표기법 (Prefix Notation) : +AB
연산자를 앞에 표기하고, 그 다음에 피연산자를 표기하는 방법이다.
중위 표기법 (Infix Notation) : A+B
연산자를 피연산자의 가운데에 표기하는 방법이다.
후위 표기법 (Postfix Notation) : AB+
연산자를 피연산자 뒤에 표기하는 방법이다.
스택을 활용하여 후위식 “8 2 / 3 - 3 2 * +”를 계산하는 과정을 그림을 통해 살펴보자.
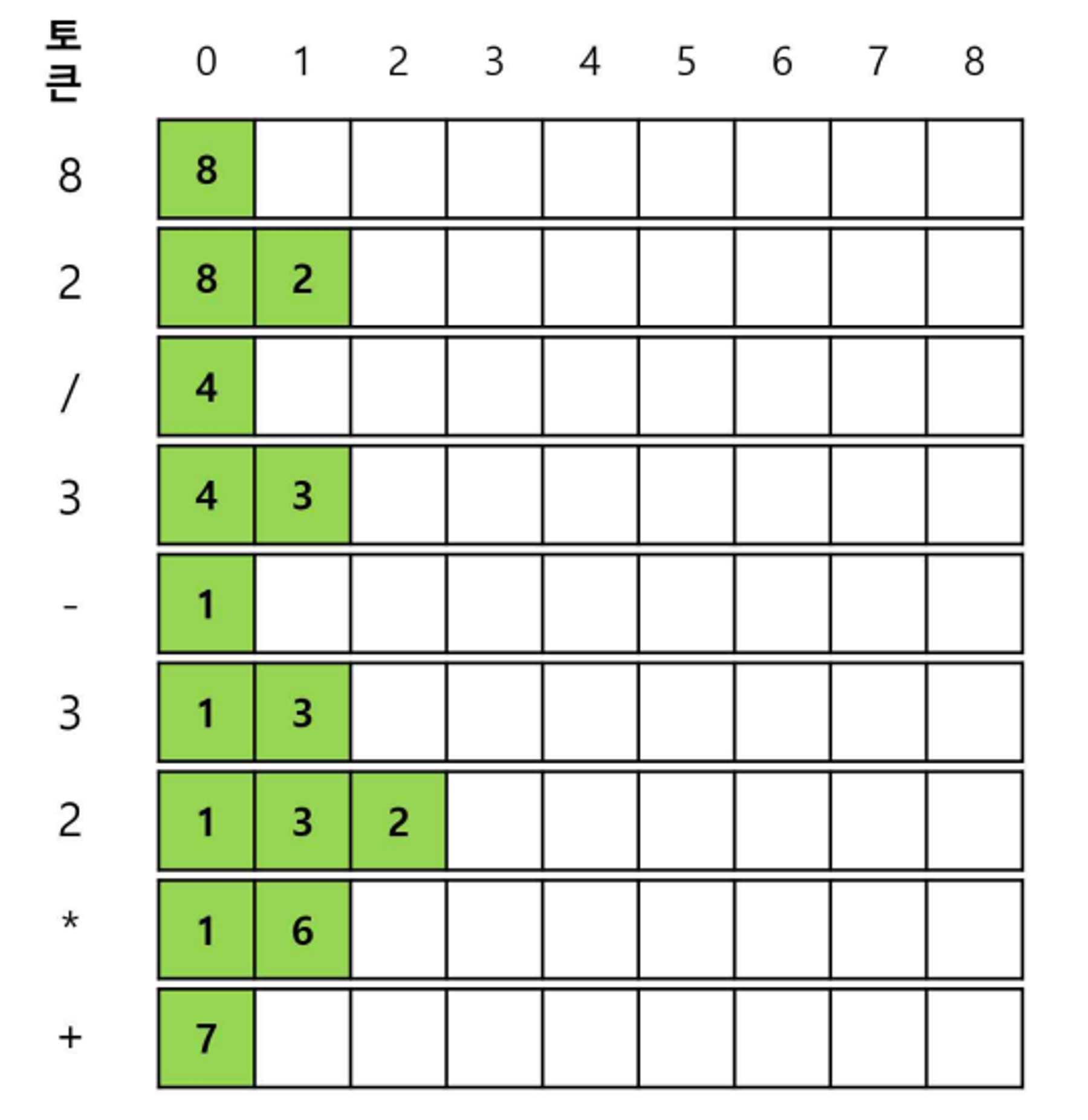
다음은 스택을 활용하여 후위 표기법으로 표현된 수식을 계산하는 알고리즘이다.
입력 : 후위 표기식 결과 : 수식 계산 결과 반환

package s240326;
import java.util.Stack;
public class FormulaTest2 {
public static void main(String[] args) {
String postfix = "82/3-32*+"; // 후위식 입력
System.out.println("후위식 : " + postfix);
evalPostfix(postfix); // 후위식 계산 결과 출력
}
public static void evalPostfix(String postfix){
char testCh=' ' ;
int expSize = postfix.length();
int num1=0, num2=0;
Stack<Integer> stack = new Stack<>(); // 자바 Stack 객체 생성
for(int i=0; i<expSize; i++){
testCh = postfix.charAt(i);
// 연산자이면 스택에서 피연산자 2개를 꺼낸후, 계산 결과를 다시 스택에 입력
if(testCh=='+' || testCh=='-' || testCh=='*' || testCh=='/'){
num2 = stack.pop();
num1 = stack.pop();
switch(testCh){
case '+' :
stack.push(num1+num2);
break;
case '-' :
stack.push(num1-num2);
break;
case '*' :
stack.push(num1*num2);
break;
case '/' :
stack.push(num1/num2);
break;
}
}else{ // 피연산자이면 스택에 푸시
stack.push(testCh-'0');
}
}
// 스택에 남은 최종 결과 출력
System.out.println("결과값 : " + stack.pop());
}
}
중위식 “2 x 3 + ( 2 - 4 ) / 2”을 후위식으로 변환하는 과정
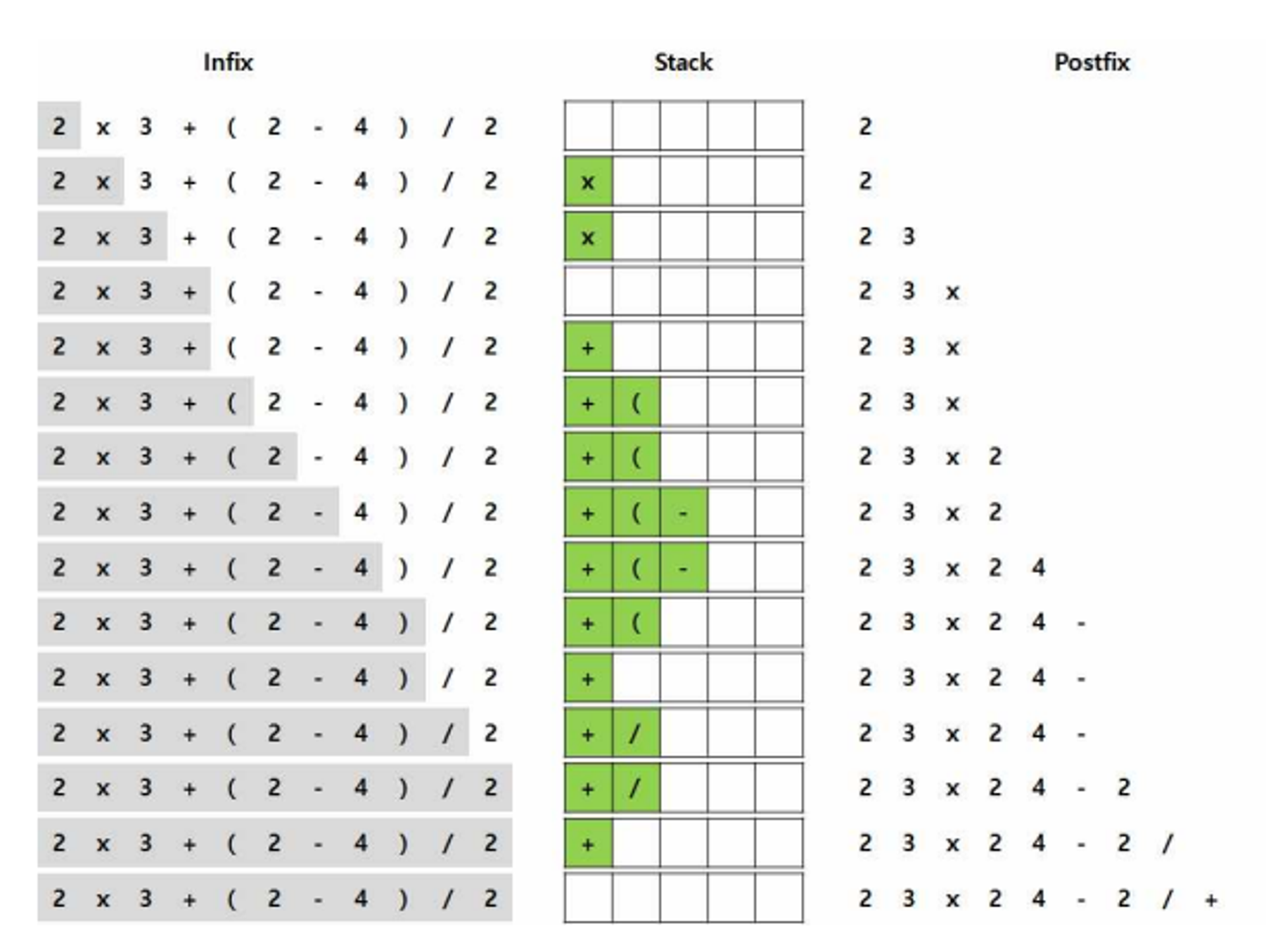
스택을 활용하여 중위식을 후위식으로 변환하는 알고리즘이다.
입력 : 중위표기식
결과 : 후위표기식 출력

package s240326;
import java.util.Stack;
public class Infix2Postfix {
public static void main(String[] args) {
String str = "2*3+(2-4)/2"; // 중위식 입력
System.out.println("중위식 : " + str);
System.out.println("후위식 : " + InToPost(str)); // 후위식 출력
}
public static String InToPost(String infixString) { // 중위식 => 후위식
Stack<String> st = new Stack<>(); // 자바 Stack 객체 생성
String postfixString = " ";
for (int index = 0; index < infixString.length(); ++index) {
char chValue = infixString.charAt(index);
if (chValue == '(') { // 여는 괄호는 무조건 스택에 푸시
st.push("(");
}
// 닫는 괄호를 만나면 스택에서 여는 괄호를 만나때 까지 팝[반복]
else if (chValue == ')') {
String oper = st.peek();
while (!(oper.equals("(")) && !(st.empty())) {
postfixString += oper;
st.pop();
oper = st.peek();
}
st.pop();
}
// 연산자는 스택의 연산자와 우선순위 비교
else if (chValue == '+' || chValue == '-') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!(st.empty() || oper.equals("(")) ||
oper.equals(")")) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else if (chValue == '*' || chValue == '/') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!oper.equals("+") && !oper.equals("-") &&
!st.empty()) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else {
postfixString += chValue;
}
}
// 스택에 남은 모든 연산자를 팝[반복]
while (!st.empty()) {
String oper = st.peek();
if (!oper.equals("(")) {
oper = st.pop();
postfixString += oper;
}
}
return postfixString;
}
}
입력 : 중위표기식 결과 : 후위표기식 출력
package s240326;
import java.util.Stack;
public class Infix2Postfix {
public static void main(String[] args) {
String str = "2*3+(2-4)/2"; // 중위식 입력
System.out.println("중위식 : " + str);
System.out.println("후위식 : " + InToPost(str)); // 후위식 출력
}
public static String InToPost(String infixString) { // 중위식 => 후위식
Stack<String> st = new Stack<>(); // 자바 Stack 객체 생성
String postfixString = " ";
for (int index = 0; index < infixString.length(); ++index) {
char chValue = infixString.charAt(index);
if (chValue == '(') { // 여는 괄호는 무조건 스택에 푸시
st.push("(");
}
// 닫는 괄호를 만나면 스택에서 여는 괄호를 만나때 까지 팝[반복]
else if (chValue == ')') {
String oper = st.peek();
while (!(oper.equals("(")) && !(st.empty())) {
postfixString += oper;
st.pop();
oper = st.peek();
}
st.pop();
}
// 연산자는 스택의 연산자와 우선순위 비교
else if (chValue == '+' || chValue == '-') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!(st.empty() || oper.equals("(")) ||
oper.equals(")")) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else if (chValue == '*' || chValue == '/') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!oper.equals("+") && !oper.equals("-") &&
!st.empty()) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else {
postfixString += chValue;
}
}
// 스택에 남은 모든 연산자를 팝[반복]
while (!st.empty()) {
String oper = st.peek();
if (!oper.equals("(")) {
oper = st.pop();
postfixString += oper;
}
}
return postfixString;
}
}
학습목표
- 스택 자료구조의 개념과 동작 방식을 이해한다.
- 배열 스택과 연결리스트 스택을 구현할 수 있다.
- 자바 Stack 클래스를 활용할 수 있다
- 괄호쌍 체크, 중위식을 후위식 변환, 후위식 계산 등 스택 응용을 구현할 수 있다.
1. 스택 개념
스택(Stack)은 ‘더미’ 또는 ‘쌓아 올림’을 의미하는 용어로, 데이터를 쌓아 올리는 형태로 저장하고 있어, 데이터를 추출할 때는 맨 위에 있는 데이터를 먼저 꺼내는 형태이다. 따라서, 스택은 제일 마지막에 저장한 데이터를 제일 먼저 꺼내는 후입선출(LIFO, Last In First Out) 형태의 자료 구조이다.
스택은 가장 마지막 데이터의 위치인 top에서 삽입이나 삭제가 발생하므로 구조적으로 한 쪽 방향에서만 입출력이 수행된다.

스택의 동작(연산)
- 삽입 연산 : push
- 삭제(추출) 연산 : pop
- 읽기 연산 : peek
2. 스택 구현
배열을 이용한 구현(배열 스택)

- 배열이 꽉 찼는지 체크를 무조건 해줘야 한다. → overflow 발생
package s240326;
class ArrayStack {
private Integer data[];
private int top;
private int maxSize;
public ArrayStack(int initsize) { // 생성자
data = new Integer[initsize];
top = 0;
maxSize = initsize;
}
public boolean empty() { // 공백 상태 체크
return top == 0;
}
public boolean full() { // 포화상태 체크
return top == maxSize;
}
public void push(Integer elem) { // push 연산
if (top == maxSize){
System.out.println("overflow"); // 스택이 꽉차면 overflow
return;
}
data[top++] = elem;
}
public Integer pop() { // pop 연산
if (top > 0)
return data[--top];
else
return null; // 스택이 비어있으면 null 반환
}
}
public class ArrayStackTest {
public static void main(String[] args) {
ArrayStack as = new ArrayStack(5); // 크기가 5인 배열 스택 생성
for (int i = 1; i <= 5; i++)
as.push(i); // 스택에 push
System.out.print("Pop : ");
for (int i = 1; i <= 5; i++)
System.out.print(as.pop()+" "); // 스택에서 pop(역순출력)
}
}
연결 리스트를 이용한 구현(연결 스택)

1 , 2 , 3 이라는 데이터를 순서대로 넣었을 때 내부에는 해당 형태로 생성되게 된다. 가장 나중에 들어간 것에 Top 포인터가 가르키고 있다.
package s240326;
class LinkedStack {
private Node top;
// 노드 class 단순연결 리스트와 같다.
private class Node{
private Integer data;
private Node nextNode;
Node(Integer data){
this.data = data;
this.nextNode = null;
}
}
// 생성자, stack이 비어있으므로 top은 null이다.
public LinkedStack(){
this.top = null;
}
// 스택이 비어있는지 확인
public boolean empty(){
return (top == null);
}
// item을 스택의 top에 넣는다.
public void push(Integer item){Node newNode = new Node(item);
newNode.nextNode = top;
top = newNode;
}
// top 노드의 데이터를 반환한다.
public Integer peek(){
if(empty()) {
System.out.println("공백상태");
return null;
}
return top.data;
}
// top 노드를 스택에서 제거한다.
public Integer pop(){
Integer item = peek();
top = top.nextNode;
return item;
}
}
public class LinkedStackTest {
public static void main(String[] args) {
LinkedStack s = new LinkedStack(); // 연결 스택 생성
for (int i = 1; i <= 5; i++)
s.push(i);
System.out.print("Pop : ");
for (int i = 1; i <= 5; i++)
System.out.print(s.pop() + " ");
}
}
자바 Stack 활용
- Stack<Integer> st = new Stack<>(); - 스택에 정수 객체를 저장할 경우
- Stack<String> st = new Stack<>(); - 스택에 String 객체를 저장할 경우
자바 Stack 클래스의 주요 메소드들은 다음과 같다
- E push(E item) : 스택의 top 위치에 item을 입력한다.
- E pop() : 스택의 top 위치에서 데이터를 추출(삭제)하여 반환한다.
- E peek() : 스택의 top 위치에서 데이터를 읽어서 반환한다. 삭제는 하지 않는다.
- boolean empty() : 스택이 비워있는지 여부를 반환한다. 빈 스택이면 true 반환.
자바 Stack 클래스는 내부적으로 연결리스트를 사용하여 구현되어 있어서 스택이 가득 차 있는지를 별도로 확인할 필요가 없다.
스택 응용
스택은 입력 데이터를 역순으로 출력하고자 하는 곳에는 모두 사용 가능한 자료구조이다.
- 수식의 괄호 검사(괄호 쌍 검사)

가장 마지막에 연 괄호를 제일 먼저 닫아 줘야하는데 우리가 생각할 수 있는 후입선출의 로직으로 pop 연산을 이용하여 꺼내면 가장 마지막에 입력된 괄호부터 pop이 되게 된다.

괄호 쌍을 체크하는 알고리즘
- 입력 : 괄호 포함 수식
- 결과 : 괄호 쌍이 맞으면 true, 실패 시 false 반환
package s240326;
import java.util.Stack;
class Formula {
private String exp;
private int expSize;
private char testCh, openPair;
public boolean checkMatching(String exp){ // 괄호쌍 체크 메소드 : 올바르면 true 반환
this.exp = exp;
Stack<Character> stack = new Stack<>(); // 문자형객체 Stack 생성
expSize = this.exp.length();
for(int i=0; i<expSize; i++){
testCh = exp.charAt(i);
switch(testCh){ // 여는 괄호면 스택에 푸시
case '(' :
case '[' :
case '{' :
stack.push(testCh); // 오토박싱, char 기초형이 Character 객체로 변환되어 저장
break;
case ')' : // 닫는 괄호면 스택에서 팝 후, 괄호쌍 매칭 검사
case ']' :
case '}' :
if(stack.empty()){
return false;
}else{
openPair = stack.pop();
if( openPair=='(' && testCh!=')' ||
openPair=='{' && testCh!='}' ||
openPair=='[' && testCh!=']' ) {
return false;
} else {
break;
}
}
}
}
if(stack.empty()) // 수식을 모두 읽은 후, 스택이 비어 있으면 오케이
return true;
else
return false;
}
}
public class FormulaTest {
public static void main(String[] args) {
Formula op = new Formula();
String exp = "{(A+B)-3}*5+[{cos(x+y)+7}-1]*4";
System.out.println(exp);
if(op.checkMatching(exp))
System.out.println("수식이 올바름(괄호의 쌍이 일치)");
else
System.out.println("수식이 올바르지 않음(괄호의 쌍이 불일치)");
}
}
- 후위식 계산
수식의 표기법에는 연산자의 위치에 따라 전위, 후위, 중위 표기법으로 나누어진다.
전위 표기법 (Prefix Notation) : +AB
연산자를 앞에 표기하고, 그 다음에 피연산자를 표기하는 방법이다.
중위 표기법 (Infix Notation) : A+B
연산자를 피연산자의 가운데에 표기하는 방법이다.
후위 표기법 (Postfix Notation) : AB+
연산자를 피연산자 뒤에 표기하는 방법이다.
스택을 활용하여 후위식 “8 2 / 3 - 3 2 * +”를 계산하는 과정을 그림을 통해 살펴보자.

다음은 스택을 활용하여 후위 표기법으로 표현된 수식을 계산하는 알고리즘이다.
입력 : 후위 표기식 결과 : 수식 계산 결과 반환

package s240326;
import java.util.Stack;
public class FormulaTest2 {
public static void main(String[] args) {
String postfix = "82/3-32*+"; // 후위식 입력
System.out.println("후위식 : " + postfix);
evalPostfix(postfix); // 후위식 계산 결과 출력
}
public static void evalPostfix(String postfix){
char testCh=' ' ;
int expSize = postfix.length();
int num1=0, num2=0;
Stack<Integer> stack = new Stack<>(); // 자바 Stack 객체 생성
for(int i=0; i<expSize; i++){
testCh = postfix.charAt(i);
// 연산자이면 스택에서 피연산자 2개를 꺼낸후, 계산 결과를 다시 스택에 입력
if(testCh=='+' || testCh=='-' || testCh=='*' || testCh=='/'){
num2 = stack.pop();
num1 = stack.pop();
switch(testCh){
case '+' :
stack.push(num1+num2);
break;
case '-' :
stack.push(num1-num2);
break;
case '*' :
stack.push(num1*num2);
break;
case '/' :
stack.push(num1/num2);
break;
}
}else{ // 피연산자이면 스택에 푸시
stack.push(testCh-'0');
}
}
// 스택에 남은 최종 결과 출력
System.out.println("결과값 : " + stack.pop());
}
}
중위식 “2 x 3 + ( 2 - 4 ) / 2”을 후위식으로 변환하는 과정

스택을 활용하여 중위식을 후위식으로 변환하는 알고리즘이다.
입력 : 중위표기식
결과 : 후위표기식 출력

package s240326;
import java.util.Stack;
public class Infix2Postfix {
public static void main(String[] args) {
String str = "2*3+(2-4)/2"; // 중위식 입력
System.out.println("중위식 : " + str);
System.out.println("후위식 : " + InToPost(str)); // 후위식 출력
}
public static String InToPost(String infixString) { // 중위식 => 후위식
Stack<String> st = new Stack<>(); // 자바 Stack 객체 생성
String postfixString = " ";
for (int index = 0; index < infixString.length(); ++index) {
char chValue = infixString.charAt(index);
if (chValue == '(') { // 여는 괄호는 무조건 스택에 푸시
st.push("(");
}
// 닫는 괄호를 만나면 스택에서 여는 괄호를 만나때 까지 팝[반복]
else if (chValue == ')') {
String oper = st.peek();
while (!(oper.equals("(")) && !(st.empty())) {
postfixString += oper;
st.pop();
oper = st.peek();
}
st.pop();
}
// 연산자는 스택의 연산자와 우선순위 비교
else if (chValue == '+' || chValue == '-') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!(st.empty() || oper.equals("(")) ||
oper.equals(")")) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else if (chValue == '*' || chValue == '/') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!oper.equals("+") && !oper.equals("-") &&
!st.empty()) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else {
postfixString += chValue;
}
}
// 스택에 남은 모든 연산자를 팝[반복]
while (!st.empty()) {
String oper = st.peek();
if (!oper.equals("(")) {
oper = st.pop();
postfixString += oper;
}
}
return postfixString;
}
}
입력 : 중위표기식 결과 : 후위표기식 출력
package s240326;
import java.util.Stack;
public class Infix2Postfix {
public static void main(String[] args) {
String str = "2*3+(2-4)/2"; // 중위식 입력
System.out.println("중위식 : " + str);
System.out.println("후위식 : " + InToPost(str)); // 후위식 출력
}
public static String InToPost(String infixString) { // 중위식 => 후위식
Stack<String> st = new Stack<>(); // 자바 Stack 객체 생성
String postfixString = " ";
for (int index = 0; index < infixString.length(); ++index) {
char chValue = infixString.charAt(index);
if (chValue == '(') { // 여는 괄호는 무조건 스택에 푸시
st.push("(");
}
// 닫는 괄호를 만나면 스택에서 여는 괄호를 만나때 까지 팝[반복]
else if (chValue == ')') {
String oper = st.peek();
while (!(oper.equals("(")) && !(st.empty())) {
postfixString += oper;
st.pop();
oper = st.peek();
}
st.pop();
}
// 연산자는 스택의 연산자와 우선순위 비교
else if (chValue == '+' || chValue == '-') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!(st.empty() || oper.equals("(")) ||
oper.equals(")")) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else if (chValue == '*' || chValue == '/') {
if (st.empty()) {
st.push(chValue + "");
} else {
String oper = st.peek();
while (!oper.equals("+") && !oper.equals("-") &&
!st.empty()) {
oper = st.pop();
postfixString += oper;
}
st.push(chValue + "");
}
} else {
postfixString += chValue;
}
}
// 스택에 남은 모든 연산자를 팝[반복]
while (!st.empty()) {
String oper = st.peek();
if (!oper.equals("(")) {
oper = st.pop();
postfixString += oper;
}
}
return postfixString;
}
}
