학습목표
- 선택정렬 알고리즘을 이해하고, 구현할 수 있다.
- 합병정렬 알고리즘을 이해하고, 구현할 수 있다.
- 퀵정렬 알고리즘을 이해하고, 구현할 수 있다.
- 이진검색 알고리즘을 이해하고, 구현할 수 있다.
- 자바의 정렬/검색 메소드를 사용할 수 있다.
1. 선택정렬(Selection Sort)

남은 것들중에서 제일 작은걸 찾아서 왼쪽에 정렬
- 선택정렬의 단계별 비교횟수의 합은(버블정렬 알고리즘 시간 복잡도) $(n-1) + (n-2) + \cdots + 1 = \frac{n(n-1)}{2} = O(n^2)$ 이다.
- 따라서 버블정렬(선택정렬)의 시간 복잡도는 $O(n^2)$ 이다.
import java.util.Arrays;
public class SelectionSort {
public static void selectionSort(int[] arr){ // 선택정렬 메소드
for (int i = 0; i < arr.length - 1; i++)
{
int index = i;
for (int j = i + 1; j < arr.length; j++) // i+1번째 최소값 찾기
if (arr[j] < arr[index])
index = j;
int smallerNumber = arr[index];
arr[index] = arr[i];
arr[i] = smallerNumber;
}
}
public static void main(String a[]){
int[] arr1 = {5, 3, 8, 1, 2, 7};
System.out.println("정렬 전 : " + Arrays.toString(arr1));
selectionSort(arr1);
System.out.println("정렬 후 : " + Arrays.toString(arr1));
}
}
- 역순으로 정렬
if (arr[j] > arr[index]) 로 변경
2. 합병정렬(Merge Sort)
리스트가 [27 10 12 20 25 13 15 22]인 경우 예를 들면,
- 분할(Divide) : 전체 배열을 (27 10 12 20), (25 13 15 22) 2개 부분배열로 분리
- 정복(Conquer) : 각 부분배열 정렬 (10 12 20 27), (13 15 22 25)
- 결합(Combine) : 2개의 정렬된 부분배열 통합 (10 12 13 15 20 22 25 27)

전체를 정렬 하려고 하면 한번에 정렬을 하는것보다 따로 정렬을 하고 합치는게 낫기 때문에 사용?
내가 정렬할 데이터가 있을 때 그 데이터가 2로 나눌 수 있을 때 사용가능하다.
개략적인 합법정렬 알고리즘
입력 : 정렬 전 리스트(배열), 정렬하고자하는 범위 [left, right]
결과 : 정렬 후 리스트
mergeSort(list, left, right) {
if (left < right) {
mid (left+right)/2;
mergeSort(list, left, mid);
mergeSort(list, mid+1, right);
merge(list, left, mid, right);
}
}

입력 : 부분 정렬된 리스트(배열), 합병 범위 [left, mid, right]
결과 : 하나로 합병된 리스트
merge(list, left, mid, right)
// 2개의 인접한 배열 list [left..mid] 와 list [mid+1..right]를 합병
i<-left:
j<-mid+1;
k<-left;
while i ≤ left and j ≤ right do
if(list[i] <list[j])
then
sorted[k] <- list[i];
k++; j++;
else
sorted[k]<-list[j];
k++; j++;
- 요소가 남아있는 부분배열을 sorted로 복사한다.
- sorted를 list로 복사한다.
합병(merge) 알고리즘의 시간복잡도는 $O(n)$이고, 합병정렬 재귀호출이 $O(logn)$ 만큼 반복 호출되므로 합병정렬 알고리즘의 시간복잡도는 $O(nlogn)$이다.
다음은 합병정렬 알고리즘을 자바로 구현한 예제이다.
import java.util.*;
public class MergeSort {
public static void main(String[] args) {
int[] a = { 27, 10, 12, 20, 25, 13, 15, 22 };
System.out.println("정렬 전 : " + Arrays.toString(a));
mergeSort(a, 0, a.length - 1);
System.out.println("정렬 후 : " + Arrays.toString(a));
}
public static void mergeSort(int[] a, int low, int high) { // 합병정렬 메소드(재귀호출)
if (low < high) {
// 중간위치 계산
int middle = low + (high - low) / 2;
// 왼쪽 리스트 합병정렬(재귀호출)
mergeSort(a, low, middle);
// 오른쪽 리스트 합병정렬(재귀호출)
mergeSort(a, middle + 1, high);
// 두 리스트 합병
merge(a, low, middle, high);
}
}
// 두 리스트 합병, [low, middle] + [middle+1, high] => [low, high]
public static void merge(int[] a, int low, int middle, int high) { // 합병 메소드
int[] sorted = new int[a.length];
int number;
// sorted 배열로 복사
for (int i = low; i <= high; i++) {
sorted[i] = a[i];
}
int i = low;
int j = middle + 1;
int k = low;
// 두 리스트의 원소 중 더 작은 원소를 sorted 배열로 복사
while (i <= middle && j <= high) {
if (sorted[i] <= sorted[j]) {
a[k] = sorted[i];
i++;
} else {
a[k] = sorted[j];
j++;
}
k++;
}
// 나머지 원소를 sorted 배열로 복사
while (i <= middle) {
a[k] = sorted[i];
k++;
i++;
}
// 두 번째 리스트의 남은 원소를 sorted 배열로 복사
while (j <= high) {
a[k] = sorted[j];
k++;
j++;
}
}
}
3. 퀵정렬(Quick Sort)
- 퀵정렬은 분할법(Partition)을 활용하는 알고리즘으로, 평균적으로 가장 빠른 정렬 알고리즘 중 하나로 알려져 있다. 이 알고리즘은 기준 값(피봇)을 중심으로 리스트(배열)를 두 개의 부분 리스트로 나누어 비균등하게 분할한다. 왼쪽 부분리스트는 기준 값보다 작은 원소들의 모임이며, 오른쪽 부분 리스트는 기준 값보다 큰 원소들의 모임이다.






위 분할 작업을 부분 리스트가 1개의 원소를 가질 때까지 반복하면 퀵정렬이 완성된다. 퀵 정렬 전체과정을 그림으로 나타내면 다음과 같다.

다음은 개략적인 퀵정렬 알고리즘이다.
입력 : 정렬 전 리스트(배열), 정렬하고자하는 범위 [low, high]
결과 : 정렬 후 리스트
void quicksort(int list [], int low, int high) {
if(low < high) {
int q-partition(list, low, high);
quickSort(list, low, q-1);
quickSort(list, q+1, high);
}
}
퀵정렬 알고리즘의 시간복잡도(Time Complexity)는 최악의 경우(리스트가 이미 정렬된 경 우)에는 $O(n^2)$ 이고, 평균적인 경우에는 $O(nlogn)$으로 매우 빠르게 정렬이 이루어진다.
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] x ={5, 3, 8, 4, 9, 1, 6, 2, 7};
System.out.println("정렬 전 : " + Arrays.toString(x));
quickSort(x, 0, x.length-1); // 퀵정렬 호출
System.out.println("정렬 후 : " + Arrays.toString(x));
}
public static int partition(int[] arr, int low, int high) { // 분할 메소드
int pivot = arr[low]; // 피봇 설정(첫번째 원소)
int i = low + 1, j = high, temp;
while (i < j) {
while (i<high && arr[i] < pivot ) // 피봇보다 큰 원소 찾기
i++;
while (j>low && arr[j] > pivot) // 피봇보다 작은 원소 찾기
j--;
if (i < j) { // 두 원소 교환
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
if ( arr[j] < arr[low] ){ // 피봇 위치를 가운데로 이동
arr[low] = arr[j];
arr[j] = pivot;
}
return j; // 피봇 최종위치 반환
}
public static void quickSort(int[] list, int low, int high) { // 퀵정렬 알고리즘(재귀호출)
if(low<high) {
int q=partition(list, low, high);
quickSort(list, low, q-1);
quickSort(list, q+1, high);
}
}
}
4. 검색(Search)
순차검색(Linear Search)
순차검색은 일렬로 된 자료(배열, 리스트)를 처음(왼편)부터 마지막(오른편) 까지 차례대로 탐색하여 찾고자하는 키 값을 검색하는 간단하고 직관적인 방법이다.
이 알고리즘의 시간복잡도는 $O(n)$으로, 검색 대상 자료가 많은 경우에는 조금 비효율적일 수 있지만, 비교적 단순하여 구현이 쉬운 특징이 있다.
public class LinearSearch {
public static int linearSearch(int[] arr, int target) { // 순차검색 메소드
for (int index = 0; index <arr.length; index++)
if (arr[index] == target)
return index;
return -1; // 찾고자 하는 데이터 없으면 -1 반환
}
public static void main(String[] args) {
int[] arr = {1,9,7,3, 5,15,10, 37, 35, 17,23, 19, 20, 25,32,31}; // 찾고자 하는 데이터가 있으면 인덱스 반환되고, 없으면 -1 반환됨
System.out.println("순차검색 결과 (23 위치) : " + linearSearch(arr, 23));
System.out.println("순차검색 결과 (21 위치) : " + linearSearch(arr, 21));
}
}
[실행결과] 순차검색 결과 (23 위치) : 10
순차검색 결과 (21 위치) : -1
이진검색(Binary Search)
이진검색(Binary Search) 알고리즘은 탐색의 대상을 절반씩 줄여 나가면서 원하는 값을 찾는 탐색 방법이다
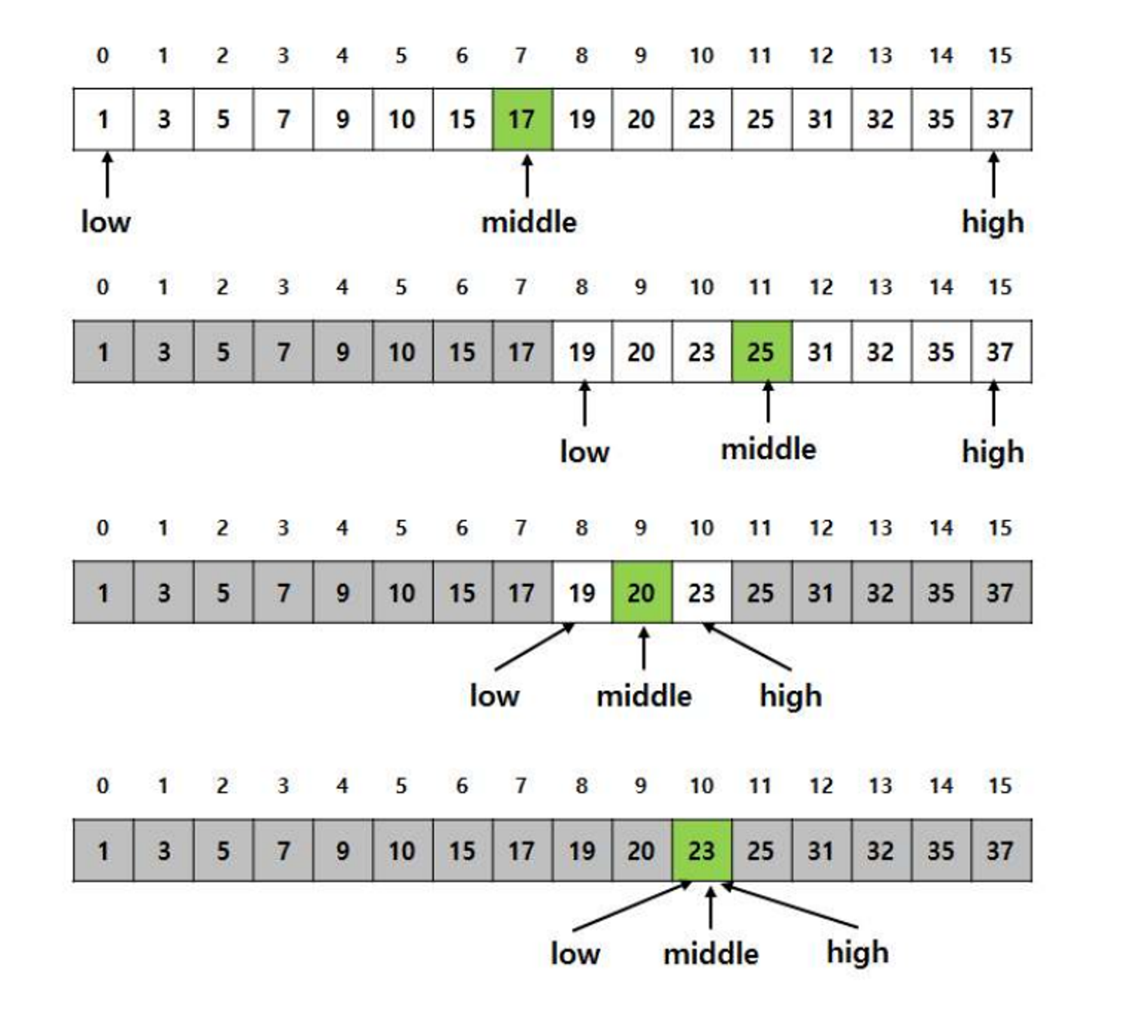
다음은 재귀적으로 표현한 이진검색 알고리즘이다. 입력 : 정렬된 리스트(배열)와 low, high 인덱스, 찾고자하는 값(key)
결과 : 찾고자하는 값이 있으면 찾은 위치(인덱스), 없으면 -1 반환
binarySearch(list, key, low, high)
middle-low에서 high사이의 중간 위치
if(key = list[middle)) return middle;
else if (key <list[middle])
return list [0] 부터 list [middle-1]에서의 탐색:
else if (key> list [middle])
return list [middle+1] 부터 list [high]에서의 탐색:
if(low>high) return -1;
이진검색 메소드는 반복문을 이용한 구현과 재귀호출을 이용한 구현 두가지 버전 모두 포함하였다.
public class BinarySearch {
public static int binarySearch(int[] a, int key) { // 이진검색 알고리즘 반복문 구현
int lo = 0;
int hi = a.length - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2; // 중악위치 계산
if (key < a[mid]) hi = mid - 1; // mid 오른쪽 범위 제거
else if (key > a[mid]) lo = mid + 1; // lo 왼쪽 범위 제거
else return mid;
}
return -1;
}
// 이진검색 알고리즘 재귀호출 구현
public static int binarySearch(int[] a, int start, int end, int target) {
int middle = (start + end) / 2;
if(end < start) {
return -1;
}
if(target==a[middle]) {
return middle;
} else if(target<a[middle]) {
return binarySearch(a, start, middle - 1, target);
} else {
return binarySearch(a, middle + 1, end, target);
}
}
public static void main(String[] args) {
int[] arr = {1,3,5,7,9,10,15,17,19,20,23,25,31,32,35,37}; // 정렬된 데이터
// 찾고자 하는 데이터가 있으면 인덱스 반환
System.out.println("이진검색 결과 (23 위치) : " + binarySearch(arr, 23));
System.out.println("이진검색 결과 (9 위치) : " + binarySearch(arr, 0, arr.length-1, 9));
}
}
[실행결과] 이진검색 결과 (23 위치) : 10
이진검색 결과 (9 위치) : 4
이진검색 알고리즘은 검색 범위를 절반씩 줄여나가면서 검색이 이루어지므로, 수행 시간 복잡도는 $O(logn)$이다. 데이터가 정렬되어 있다면, 검색 시 이진검색 알고리즘을 적용하면 매우 빠르게 검색이 가능하다.
5. 자바 정렬/검색 메소드 활용
자바 API에 포함된 정렬/검색 메소드는 자료구조의 종류에 따라 각각 다르게 구현되어 있다. 데이터 가 배열에 저장되어 있다면 Arrays 클래스에 포함된 메소드로 정렬과 검색이 가능하고, 데이터가 컬렉션 객체(ArrayList, LinkedList, Stack, Queue 등)에 저장되어 있다면 Collections 클래스에 포함된 메소드로 정렬과 검색이 가능하다.
Arrays 클래스를 활용한 정렬/검색
static void sort(int[] a) int형 배열 a를 오름차순 정렬수행(double, Object, String 등 배열에 대해서는 중복정의 되어 있음) 객체를 정렬하기 위해선 객체가 Comparable 인터페이스를 구현해야한다.
예) int[] arr = {9, 3, 5, 7, 1};
Arrays.sort(arr); // [1, 3, 5, 7, 9]로 정렬됨
static int binarySearch(int[] a, int key) int형 정렬된 배열 a에서 key값을 이진검색하여 위치 반환(모든 형에 대해 중복정의)
예) int[] arr = {1, 3, 5, 7, 9};
System.out.print(Arrays.binarySearch(arr, 5)); // 인덱스 2 반환
static void fill(int[] a, int val) int형 배열 a의 모든 원소를 val 값으로 초기화 시킴(모든 형에 대해 중복정의)
예) int[] arr = new int[10];
Arrays.fill(arr, 1); // 모든 원소를 1로 초기화
static boolean equals(int[] a, int[] b) int형 배열 a와 b의 모든 원소가 같으면 true, 아니면 false 반환(모든 형에 대해 중복정의)
예) int[] a = {1, 3, 5, 7, 9};
int[] b= {1, 3, 5, 7, 9}; System.out.print(Arrays.equals(a, b)); // 배열 비교, true 출력
static <T> List<T> asList(T... a) 배열을 컬렉션 타입인 리스트로 변환(포장) 리스트 객체의 메소드를 적용가능 하지만 원본은 배열이어서 크기가 늘어나지는 않음
예) List<String> list1 = Arrays.asList("nice", "to", "meet", "you"};
Integer[] arr = {1, 2, 3, 4, 5};
List<Integer> list2 = Arrays.asList(arr);
Arrays 클래스의 주요 메소드를 활용하는 예제이다.
import java.util.Arrays;
import java.util.Collections;
public class ArrayTest0 {
public static void main(String[] args) {
String[] str={"나", "사", "아", "마", "바", "다", "라", "가"};
System.out.println("정렬 전 : " + Arrays.toString(str)); // 배열 원소 출력
Arrays.sort(str); // 오름차순 정렬(기본)
System.out.println("오름차순 정렬 후 : "+ Arrays.toString(str));
Arrays.sort(str, Collections.reverseOrder()); // 내림차순 정렬
System.out.println("내림차순 정렬 후 : "+ Arrays.toString(str));
}
}
[실행결과]
정렬 전 : [나, 사, 아, 마, 바, 다, 라, 가]
오름차순 정렬 후 : [가, 나, 다, 라, 마, 바, 사, 아]
내림차순 정렬 후 : [아, 사, 바, 마, 라, 다, 나, 가]
다음은 사용자정의클래스 타입의 객체를 저장하는 리스트 객체에 Collections 클래스 메소드를 사용하여 정렬/검색을 수행한 예제이다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
class Song implements Comparable<Song> { // Song 클래스 정의
private String title;
private String author;
private int rank;
public Song(String title, String author, int rank) { // 생성자
super();
this.title = title;
this.author = author;
this.rank = rank;
}
public String getTitle() { return title; }
public void setTitle(String title) { this.title = title; }
public String getAuthor() { return author; }
public void setAuthor(String author) { this.author = author; }
public int getRank() { return rank; }
public void setRank(int rank) { this.rank = rank; }
public int compareTo(Song o) { // 정렬 기준 설정 : 랭킹
return this.rank - o.rank;
}
}
public class SongSortTest {
public static void main(String[] args) {
List<Song> songList = new ArrayList<>(); // 리스트 객체 생성
songList.add(new Song("끝", "권진아", 4));
songList.add(new Song("구르미 그린 달빛", "거미", 2));
songList.add(new Song("이소설의 끝을 다시 써보려해 ", "한동근", 3));
songList.add(new Song("다정하게,안녕히", "성시경", 5));
songList.add(new Song("내가 저지른 사랑", "임창정", 1));
System.out.println("정렬 전 ---------------------");
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
System.out.println("정렬 후 ---------------------");
Collections.sort(songList); // 리스트 객체 정렬
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
System.out.println("역순출력 -------------------");
Collections.reverse(songList); // 리스트 객체 역순 만들기
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
}
}
[실행결과]
정렬전--------------------- 끝, 권진아, 4위
구르미 그린 달빛, 거미, 2위
이소설의 끝을 다시 써보려해 , 한동근, 3위
다정하게,안녕히, 성시경, 5위
내가 저지른 사랑, 임창정, 1위
정렬후--------------------- 내가 저지른 사랑, 임창정, 1위
구르미 그린 달빛, 거미, 2위
이소설의 끝을 다시 써보려해 , 한동근, 3위
끝, 권진아, 4위
다정하게,안녕히, 성시경, 5위
역순정렬------------------- 다정하게,안녕히, 성시경, 5위
끝, 권진아, 4위
이소설의 끝을 다시 써보려해 , 한동근, 3위
구르미 그린 달빛, 거미, 2위
내가 저지른 사랑, 임창정, 1위
연습문제
1~100사이의 임의의 정수 20개를 생성하여 배열에 저장한 후, 사용자 로부터 찾은 키 값을 입력받아 이진검색을 수행하는 프로그램을 작성하 시오.
import java.util.Arrays;
import java.util.Random;
import java.util.Scanner;
/*
* 1~100사이의 임의의 정수 20개를 생성하여 배열에 저장한 후, 사용자
로부터 찾은 키 값을 입력받아 이진검색을 수행하는 프로그램을 작성하
시오.
* */
class BinSearch {
public static int binarySearch(int[] a, int key) { // 이진검색 알고리즘 반복문 구현
int lo = 0;
int hi = a.length - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2; // 중악위치 계산
if (key < a[mid]) hi = mid - 1; // mid 오른쪽 범위 제거
else if (key > a[mid]) lo = mid + 1; // lo 왼쪽 범위 제거
else return mid;
}
return -1;
}
// 이진검색 알고리즘 재귀호출 구현
public static int binarySearch(int[] a, int start, int end, int target) {
int middle = (start + end) / 2;
if (end < start) {
return -1;
}
if (target == a[middle]) {
return middle;
} else if (target < a[middle]) {
return binarySearch(a, start, middle - 1, target);
} else {
return binarySearch(a, middle + 1, end, target);
}
}
}
public class RandomTest {
public static void main(String[] args) {
Random rd = new Random();
int[] array = new int[20];
for (int i = 0; i < array.length; i++) {
array[i] = rd.nextInt(100) + 1; // 1~100사이의 랜덤한 정수 생성
}
Arrays.sort(array);
System.out.print("배열의 정보 {");
for (int j = 0; j<array.length; j++) {
System.out.print(array[j] + " ");
}
System.out.println("}");
Scanner sc = new Scanner(System.in);
System.out.print("찾을 키 값을 입력해주세요. ");
int key = sc.nextInt();
System.out.printf("이진검색 결과 (%d 위치) : " + BinSearch.binarySearch(array, key) + "\\n", key);
System.out.println("찾을 키 값을 입력해주세요.");
int key2 = sc.nextInt();
System.out.printf("이진검색 결과 (%d 위치) : " + BinSearch.binarySearch(array,0, array.length-1 ,key2) , key2);
}
}
학습목표
- 선택정렬 알고리즘을 이해하고, 구현할 수 있다.
- 합병정렬 알고리즘을 이해하고, 구현할 수 있다.
- 퀵정렬 알고리즘을 이해하고, 구현할 수 있다.
- 이진검색 알고리즘을 이해하고, 구현할 수 있다.
- 자바의 정렬/검색 메소드를 사용할 수 있다.
1. 선택정렬(Selection Sort)

남은 것들중에서 제일 작은걸 찾아서 왼쪽에 정렬
- 선택정렬의 단계별 비교횟수의 합은(버블정렬 알고리즘 시간 복잡도) 이다.
- 따라서 버블정렬(선택정렬)의 시간 복잡도는 이다.
import java.util.Arrays;
public class SelectionSort {
public static void selectionSort(int[] arr){ // 선택정렬 메소드
for (int i = 0; i < arr.length - 1; i++)
{
int index = i;
for (int j = i + 1; j < arr.length; j++) // i+1번째 최소값 찾기
if (arr[j] < arr[index])
index = j;
int smallerNumber = arr[index];
arr[index] = arr[i];
arr[i] = smallerNumber;
}
}
public static void main(String a[]){
int[] arr1 = {5, 3, 8, 1, 2, 7};
System.out.println("정렬 전 : " + Arrays.toString(arr1));
selectionSort(arr1);
System.out.println("정렬 후 : " + Arrays.toString(arr1));
}
}
- 역순으로 정렬
if (arr[j] > arr[index]) 로 변경
2. 합병정렬(Merge Sort)
리스트가 [27 10 12 20 25 13 15 22]인 경우 예를 들면,
- 분할(Divide) : 전체 배열을 (27 10 12 20), (25 13 15 22) 2개 부분배열로 분리
- 정복(Conquer) : 각 부분배열 정렬 (10 12 20 27), (13 15 22 25)
- 결합(Combine) : 2개의 정렬된 부분배열 통합 (10 12 13 15 20 22 25 27)

전체를 정렬 하려고 하면 한번에 정렬을 하는것보다 따로 정렬을 하고 합치는게 낫기 때문에 사용?
내가 정렬할 데이터가 있을 때 그 데이터가 2로 나눌 수 있을 때 사용가능하다.
개략적인 합법정렬 알고리즘
입력 : 정렬 전 리스트(배열), 정렬하고자하는 범위 [left, right]
결과 : 정렬 후 리스트
mergeSort(list, left, right) {
if (left < right) {
mid (left+right)/2;
mergeSort(list, left, mid);
mergeSort(list, mid+1, right);
merge(list, left, mid, right);
}
}

입력 : 부분 정렬된 리스트(배열), 합병 범위 [left, mid, right]
결과 : 하나로 합병된 리스트
merge(list, left, mid, right)
// 2개의 인접한 배열 list [left..mid] 와 list [mid+1..right]를 합병
i<-left:
j<-mid+1;
k<-left;
while i ≤ left and j ≤ right do
if(list[i] <list[j])
then
sorted[k] <- list[i];
k++; j++;
else
sorted[k]<-list[j];
k++; j++;
- 요소가 남아있는 부분배열을 sorted로 복사한다.
- sorted를 list로 복사한다.
합병(merge) 알고리즘의 시간복잡도는 이고, 합병정렬 재귀호출이 만큼 반복 호출되므로 합병정렬 알고리즘의 시간복잡도는 이다.
다음은 합병정렬 알고리즘을 자바로 구현한 예제이다.
import java.util.*;
public class MergeSort {
public static void main(String[] args) {
int[] a = { 27, 10, 12, 20, 25, 13, 15, 22 };
System.out.println("정렬 전 : " + Arrays.toString(a));
mergeSort(a, 0, a.length - 1);
System.out.println("정렬 후 : " + Arrays.toString(a));
}
public static void mergeSort(int[] a, int low, int high) { // 합병정렬 메소드(재귀호출)
if (low < high) {
// 중간위치 계산
int middle = low + (high - low) / 2;
// 왼쪽 리스트 합병정렬(재귀호출)
mergeSort(a, low, middle);
// 오른쪽 리스트 합병정렬(재귀호출)
mergeSort(a, middle + 1, high);
// 두 리스트 합병
merge(a, low, middle, high);
}
}
// 두 리스트 합병, [low, middle] + [middle+1, high] => [low, high]
public static void merge(int[] a, int low, int middle, int high) { // 합병 메소드
int[] sorted = new int[a.length];
int number;
// sorted 배열로 복사
for (int i = low; i <= high; i++) {
sorted[i] = a[i];
}
int i = low;
int j = middle + 1;
int k = low;
// 두 리스트의 원소 중 더 작은 원소를 sorted 배열로 복사
while (i <= middle && j <= high) {
if (sorted[i] <= sorted[j]) {
a[k] = sorted[i];
i++;
} else {
a[k] = sorted[j];
j++;
}
k++;
}
// 나머지 원소를 sorted 배열로 복사
while (i <= middle) {
a[k] = sorted[i];
k++;
i++;
}
// 두 번째 리스트의 남은 원소를 sorted 배열로 복사
while (j <= high) {
a[k] = sorted[j];
k++;
j++;
}
}
}
3. 퀵정렬(Quick Sort)
- 퀵정렬은 분할법(Partition)을 활용하는 알고리즘으로, 평균적으로 가장 빠른 정렬 알고리즘 중 하나로 알려져 있다. 이 알고리즘은 기준 값(피봇)을 중심으로 리스트(배열)를 두 개의 부분 리스트로 나누어 비균등하게 분할한다. 왼쪽 부분리스트는 기준 값보다 작은 원소들의 모임이며, 오른쪽 부분 리스트는 기준 값보다 큰 원소들의 모임이다.






위 분할 작업을 부분 리스트가 1개의 원소를 가질 때까지 반복하면 퀵정렬이 완성된다. 퀵 정렬 전체과정을 그림으로 나타내면 다음과 같다.

다음은 개략적인 퀵정렬 알고리즘이다.
입력 : 정렬 전 리스트(배열), 정렬하고자하는 범위 [low, high]
결과 : 정렬 후 리스트
void quicksort(int list [], int low, int high) {
if(low < high) {
int q-partition(list, low, high);
quickSort(list, low, q-1);
quickSort(list, q+1, high);
}
}
퀵정렬 알고리즘의 시간복잡도(Time Complexity)는 최악의 경우(리스트가 이미 정렬된 경 우)에는 이고, 평균적인 경우에는 으로 매우 빠르게 정렬이 이루어진다.
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] x ={5, 3, 8, 4, 9, 1, 6, 2, 7};
System.out.println("정렬 전 : " + Arrays.toString(x));
quickSort(x, 0, x.length-1); // 퀵정렬 호출
System.out.println("정렬 후 : " + Arrays.toString(x));
}
public static int partition(int[] arr, int low, int high) { // 분할 메소드
int pivot = arr[low]; // 피봇 설정(첫번째 원소)
int i = low + 1, j = high, temp;
while (i < j) {
while (i<high && arr[i] < pivot ) // 피봇보다 큰 원소 찾기
i++;
while (j>low && arr[j] > pivot) // 피봇보다 작은 원소 찾기
j--;
if (i < j) { // 두 원소 교환
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
if ( arr[j] < arr[low] ){ // 피봇 위치를 가운데로 이동
arr[low] = arr[j];
arr[j] = pivot;
}
return j; // 피봇 최종위치 반환
}
public static void quickSort(int[] list, int low, int high) { // 퀵정렬 알고리즘(재귀호출)
if(low<high) {
int q=partition(list, low, high);
quickSort(list, low, q-1);
quickSort(list, q+1, high);
}
}
}
4. 검색(Search)
순차검색(Linear Search)
순차검색은 일렬로 된 자료(배열, 리스트)를 처음(왼편)부터 마지막(오른편) 까지 차례대로 탐색하여 찾고자하는 키 값을 검색하는 간단하고 직관적인 방법이다.
이 알고리즘의 시간복잡도는 으로, 검색 대상 자료가 많은 경우에는 조금 비효율적일 수 있지만, 비교적 단순하여 구현이 쉬운 특징이 있다.
public class LinearSearch {
public static int linearSearch(int[] arr, int target) { // 순차검색 메소드
for (int index = 0; index <arr.length; index++)
if (arr[index] == target)
return index;
return -1; // 찾고자 하는 데이터 없으면 -1 반환
}
public static void main(String[] args) {
int[] arr = {1,9,7,3, 5,15,10, 37, 35, 17,23, 19, 20, 25,32,31}; // 찾고자 하는 데이터가 있으면 인덱스 반환되고, 없으면 -1 반환됨
System.out.println("순차검색 결과 (23 위치) : " + linearSearch(arr, 23));
System.out.println("순차검색 결과 (21 위치) : " + linearSearch(arr, 21));
}
}
[실행결과] 순차검색 결과 (23 위치) : 10
순차검색 결과 (21 위치) : -1
이진검색(Binary Search)
이진검색(Binary Search) 알고리즘은 탐색의 대상을 절반씩 줄여 나가면서 원하는 값을 찾는 탐색 방법이다

다음은 재귀적으로 표현한 이진검색 알고리즘이다. 입력 : 정렬된 리스트(배열)와 low, high 인덱스, 찾고자하는 값(key)
결과 : 찾고자하는 값이 있으면 찾은 위치(인덱스), 없으면 -1 반환
binarySearch(list, key, low, high)
middle-low에서 high사이의 중간 위치
if(key = list[middle)) return middle;
else if (key <list[middle])
return list [0] 부터 list [middle-1]에서의 탐색:
else if (key> list [middle])
return list [middle+1] 부터 list [high]에서의 탐색:
if(low>high) return -1;
이진검색 메소드는 반복문을 이용한 구현과 재귀호출을 이용한 구현 두가지 버전 모두 포함하였다.
public class BinarySearch {
public static int binarySearch(int[] a, int key) { // 이진검색 알고리즘 반복문 구현
int lo = 0;
int hi = a.length - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2; // 중악위치 계산
if (key < a[mid]) hi = mid - 1; // mid 오른쪽 범위 제거
else if (key > a[mid]) lo = mid + 1; // lo 왼쪽 범위 제거
else return mid;
}
return -1;
}
// 이진검색 알고리즘 재귀호출 구현
public static int binarySearch(int[] a, int start, int end, int target) {
int middle = (start + end) / 2;
if(end < start) {
return -1;
}
if(target==a[middle]) {
return middle;
} else if(target<a[middle]) {
return binarySearch(a, start, middle - 1, target);
} else {
return binarySearch(a, middle + 1, end, target);
}
}
public static void main(String[] args) {
int[] arr = {1,3,5,7,9,10,15,17,19,20,23,25,31,32,35,37}; // 정렬된 데이터
// 찾고자 하는 데이터가 있으면 인덱스 반환
System.out.println("이진검색 결과 (23 위치) : " + binarySearch(arr, 23));
System.out.println("이진검색 결과 (9 위치) : " + binarySearch(arr, 0, arr.length-1, 9));
}
}
[실행결과] 이진검색 결과 (23 위치) : 10
이진검색 결과 (9 위치) : 4
이진검색 알고리즘은 검색 범위를 절반씩 줄여나가면서 검색이 이루어지므로, 수행 시간 복잡도는 이다. 데이터가 정렬되어 있다면, 검색 시 이진검색 알고리즘을 적용하면 매우 빠르게 검색이 가능하다.
5. 자바 정렬/검색 메소드 활용
자바 API에 포함된 정렬/검색 메소드는 자료구조의 종류에 따라 각각 다르게 구현되어 있다. 데이터 가 배열에 저장되어 있다면 Arrays 클래스에 포함된 메소드로 정렬과 검색이 가능하고, 데이터가 컬렉션 객체(ArrayList, LinkedList, Stack, Queue 등)에 저장되어 있다면 Collections 클래스에 포함된 메소드로 정렬과 검색이 가능하다.
Arrays 클래스를 활용한 정렬/검색
static void sort(int[] a) int형 배열 a를 오름차순 정렬수행(double, Object, String 등 배열에 대해서는 중복정의 되어 있음) 객체를 정렬하기 위해선 객체가 Comparable 인터페이스를 구현해야한다.
예) int[] arr = {9, 3, 5, 7, 1};
Arrays.sort(arr); // [1, 3, 5, 7, 9]로 정렬됨
static int binarySearch(int[] a, int key) int형 정렬된 배열 a에서 key값을 이진검색하여 위치 반환(모든 형에 대해 중복정의)
예) int[] arr = {1, 3, 5, 7, 9};
System.out.print(Arrays.binarySearch(arr, 5)); // 인덱스 2 반환
static void fill(int[] a, int val) int형 배열 a의 모든 원소를 val 값으로 초기화 시킴(모든 형에 대해 중복정의)
예) int[] arr = new int[10];
Arrays.fill(arr, 1); // 모든 원소를 1로 초기화
static boolean equals(int[] a, int[] b) int형 배열 a와 b의 모든 원소가 같으면 true, 아니면 false 반환(모든 형에 대해 중복정의)
예) int[] a = {1, 3, 5, 7, 9};
int[] b= {1, 3, 5, 7, 9}; System.out.print(Arrays.equals(a, b)); // 배열 비교, true 출력
static <T> List<T> asList(T... a) 배열을 컬렉션 타입인 리스트로 변환(포장) 리스트 객체의 메소드를 적용가능 하지만 원본은 배열이어서 크기가 늘어나지는 않음
예) List<String> list1 = Arrays.asList("nice", "to", "meet", "you"};
Integer[] arr = {1, 2, 3, 4, 5};
List<Integer> list2 = Arrays.asList(arr);
Arrays 클래스의 주요 메소드를 활용하는 예제이다.
import java.util.Arrays;
import java.util.Collections;
public class ArrayTest0 {
public static void main(String[] args) {
String[] str={"나", "사", "아", "마", "바", "다", "라", "가"};
System.out.println("정렬 전 : " + Arrays.toString(str)); // 배열 원소 출력
Arrays.sort(str); // 오름차순 정렬(기본)
System.out.println("오름차순 정렬 후 : "+ Arrays.toString(str));
Arrays.sort(str, Collections.reverseOrder()); // 내림차순 정렬
System.out.println("내림차순 정렬 후 : "+ Arrays.toString(str));
}
}
[실행결과]
정렬 전 : [나, 사, 아, 마, 바, 다, 라, 가]
오름차순 정렬 후 : [가, 나, 다, 라, 마, 바, 사, 아]
내림차순 정렬 후 : [아, 사, 바, 마, 라, 다, 나, 가]
다음은 사용자정의클래스 타입의 객체를 저장하는 리스트 객체에 Collections 클래스 메소드를 사용하여 정렬/검색을 수행한 예제이다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
class Song implements Comparable<Song> { // Song 클래스 정의
private String title;
private String author;
private int rank;
public Song(String title, String author, int rank) { // 생성자
super();
this.title = title;
this.author = author;
this.rank = rank;
}
public String getTitle() { return title; }
public void setTitle(String title) { this.title = title; }
public String getAuthor() { return author; }
public void setAuthor(String author) { this.author = author; }
public int getRank() { return rank; }
public void setRank(int rank) { this.rank = rank; }
public int compareTo(Song o) { // 정렬 기준 설정 : 랭킹
return this.rank - o.rank;
}
}
public class SongSortTest {
public static void main(String[] args) {
List<Song> songList = new ArrayList<>(); // 리스트 객체 생성
songList.add(new Song("끝", "권진아", 4));
songList.add(new Song("구르미 그린 달빛", "거미", 2));
songList.add(new Song("이소설의 끝을 다시 써보려해 ", "한동근", 3));
songList.add(new Song("다정하게,안녕히", "성시경", 5));
songList.add(new Song("내가 저지른 사랑", "임창정", 1));
System.out.println("정렬 전 ---------------------");
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
System.out.println("정렬 후 ---------------------");
Collections.sort(songList); // 리스트 객체 정렬
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
System.out.println("역순출력 -------------------");
Collections.reverse(songList); // 리스트 객체 역순 만들기
for (Song song : songList)
System.out.println(song.getTitle() + ", " + song.getAuthor() + ", "
+ song.getRank() + "위");
}
}
[실행결과]
정렬전--------------------- 끝, 권진아, 4위
구르미 그린 달빛, 거미, 2위
이소설의 끝을 다시 써보려해 , 한동근, 3위
다정하게,안녕히, 성시경, 5위
내가 저지른 사랑, 임창정, 1위
정렬후--------------------- 내가 저지른 사랑, 임창정, 1위
구르미 그린 달빛, 거미, 2위
이소설의 끝을 다시 써보려해 , 한동근, 3위
끝, 권진아, 4위
다정하게,안녕히, 성시경, 5위
역순정렬------------------- 다정하게,안녕히, 성시경, 5위
끝, 권진아, 4위
이소설의 끝을 다시 써보려해 , 한동근, 3위
구르미 그린 달빛, 거미, 2위
내가 저지른 사랑, 임창정, 1위
연습문제
1~100사이의 임의의 정수 20개를 생성하여 배열에 저장한 후, 사용자 로부터 찾은 키 값을 입력받아 이진검색을 수행하는 프로그램을 작성하 시오.
import java.util.Arrays;
import java.util.Random;
import java.util.Scanner;
/*
* 1~100사이의 임의의 정수 20개를 생성하여 배열에 저장한 후, 사용자
로부터 찾은 키 값을 입력받아 이진검색을 수행하는 프로그램을 작성하
시오.
* */
class BinSearch {
public static int binarySearch(int[] a, int key) { // 이진검색 알고리즘 반복문 구현
int lo = 0;
int hi = a.length - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2; // 중악위치 계산
if (key < a[mid]) hi = mid - 1; // mid 오른쪽 범위 제거
else if (key > a[mid]) lo = mid + 1; // lo 왼쪽 범위 제거
else return mid;
}
return -1;
}
// 이진검색 알고리즘 재귀호출 구현
public static int binarySearch(int[] a, int start, int end, int target) {
int middle = (start + end) / 2;
if (end < start) {
return -1;
}
if (target == a[middle]) {
return middle;
} else if (target < a[middle]) {
return binarySearch(a, start, middle - 1, target);
} else {
return binarySearch(a, middle + 1, end, target);
}
}
}
public class RandomTest {
public static void main(String[] args) {
Random rd = new Random();
int[] array = new int[20];
for (int i = 0; i < array.length; i++) {
array[i] = rd.nextInt(100) + 1; // 1~100사이의 랜덤한 정수 생성
}
Arrays.sort(array);
System.out.print("배열의 정보 {");
for (int j = 0; j<array.length; j++) {
System.out.print(array[j] + " ");
}
System.out.println("}");
Scanner sc = new Scanner(System.in);
System.out.print("찾을 키 값을 입력해주세요. ");
int key = sc.nextInt();
System.out.printf("이진검색 결과 (%d 위치) : " + BinSearch.binarySearch(array, key) + "\\n", key);
System.out.println("찾을 키 값을 입력해주세요.");
int key2 = sc.nextInt();
System.out.printf("이진검색 결과 (%d 위치) : " + BinSearch.binarySearch(array,0, array.length-1 ,key2) , key2);
}
}
