학습목표
- 정점, 간선, 경로, 차수 등 그래프 관련 용어를 이해한다.
- 인접 행렬, 인접 리스트로 그래프를 표현할 수 있다.
- DFS 알고리즘을 이해하고, 구현할 수 있다.
- BFS 알고리즘을 이해하고, 구현할 수 있다.
1. 그래프 개념
그래프 정의
그래프는 현실 세계의 다양한 관계를 표현하는 자료구조로, 여러 개의 노드(node) 또는 정점(vertex)이 간선(edge)으로 연결되어 있는 구조이다. 도로망, 지인 관계, 링크 관계, 프로세스와 자원 간의 관계 등을 그래프로 모델링할 수 있어 다양한 분야에서 활용된다. 그래프는 방향성과 순환성에 따라 다양한 종류의 그래프로 나뉘며, 이를 통해 다양한 문제들을 해결할 수 있다.
그래프 구성요소
그래프는 정점(Node, Vertex)과 간선(Edge) 들의 집합으로 구성된다. 간선은 정점간의 관계 나타내며 비용, 거리 등 가중치 값을 가질 수 있다.

위 그래프 G=(V, E)의 구성요소는 다음과 같다.
(V는 정점 집합, E는 간선집합)
V = {0, 1, 2, 3, 4, 5, 6}
E = {(0,1), (0,5), (1,2), (1,6), (2,3), (3,4), (3,6), (4,5), (4,6)}
도시 : 정점
도로끼리를 잇는 도로 : 간선
가중치는 있을 수도 있고 없을 수도 있음
배열표현법 → 2차원(인접 행렬, 인접 리스트)
그래프의 종류
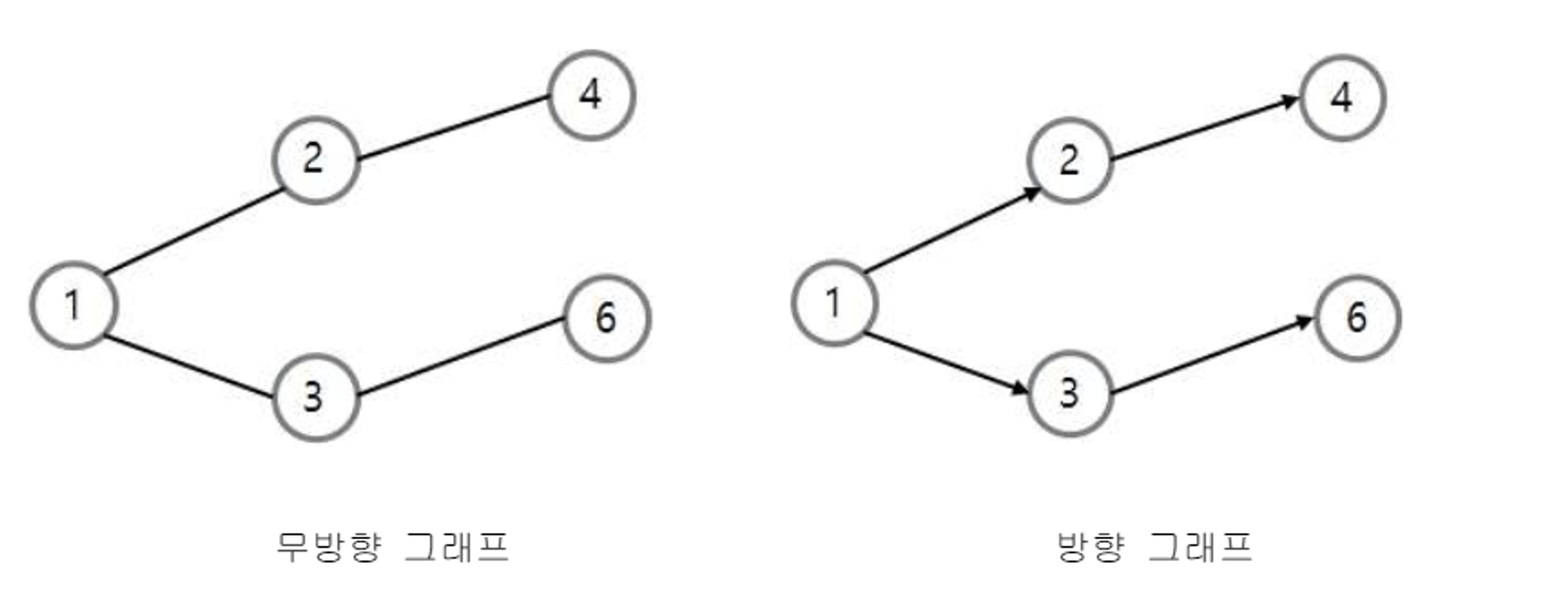
가중치 그래프는 간선에 가중치가 있는 그래프이다. 정점 이동 간에 드는 비용이나, 거리등을 가중치로 표현한다.

그래프 경로(Path)와 사이클(Cycle)
경로란 연결 가능한 간선들의 순서 열이다. 아래의 그래프에서 (1, 2, 4, 5)는 정점 1에서 정점 5로 가는 경로가 맞지만, (1, 2, 3)은 간선 <2, 3>이 없으므로 경로가 아니다.

사이클은 같은 정점으로 되돌아오는 경로이다.
위 그래프에서 (1, 2, 4, 3, 1)은 정점 1에서 출발해서, 정점 1로 되돌아 오기 때문에 사이클이다.
만약 6을 방문하고 싶을때 순서는 1 → 2 → 4 → 3 → 1 → 이런식으로 무한루프가 발생할 수 도 있음
그래프에서는 사이클을 체크하는것, 피해가는게 굉장히 중요하다.
그래프의 표현
그래프 자료구조를 메모리에 표현하는 방법은 다른 자료구조와 마찬가지로 배열을 이용하는 방법(인접 행렬)과 연결리스트를 이용하는 방법(인접 리스트)이 있다.
인접 행렬(Adjacent Matrix)

간선이 있으면 1, 없으면 0 → 그래서 2차원이 될 수 밖에 없음
무방향 그래프를 인접 행렬로 표현하는 예제
import java.util.Scanner;
// 무방향 그래프를 인접 행렬로 표현
public class GraphTest1 {
static int nE;
static int nV;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nV = scan.nextInt(); // Vertex (정점)
nE = scan.nextInt(); // Edge (간선)
// Vertex의 이름을 그대로 사용하기 위해 (nV+1)(nV+1)개만큼 배열 생성
int[][] ad = new int[nV+1][nV+1];
for(int i = 0; i < nE; i++){ // Edge 정보 입력 받음
int t1 = scan.nextInt();
int t2 = scan.nextInt();
ad[t1][t2] = ad[t2][t1] = 1; // 1대신 가중치를 넣으면 가중치 그래프
}
}
}
인접 리스트(Adjacent List)
그래프를 표현하는 두 번째 방법은 연결리스트를 이용하는 방법이다. 이를, 인접 리스트라한다.
인접 리스트 방식에서는 정점의 수만큼 연결리스트를 생성하고, 각 정점 연결리스트에 연결된 정점을 추가한다
무방향 그래프를 인접 리스트로 표현한 그림

리스트 개수가 정점 개수만큼 생긴다.
그래프의 각 정점마다 해당 정점에서 나가는 간선의 목록을 저장하기위해 각 정점마다 하나의 연결리스트를 갖는 방식으로 구현한다.
무방향 그래프를 인접 리스트로 표현하는 예제
public class GraphTest2 {
static int nV; // 총 vertex 개수
static int nE; // 총 edge 개
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nV = scan.nextInt();
nE = scan.nextInt();
// 인접 리스트 초기화
ArrayList<ArrayList<Integer>> ad = new ArrayList<>();
for(int i = 0; i < nV; i++) { // 정점 개수만큼 ArrayList 생성
ad.add(new<Integer> ArrayList()); // ad 리스트에 담을 리스트 초기화
}
for(int i = 0; i < nE; i++) {
int t1, t2; // vertex 두 개 입력 받기
t1 = scan.nextInt(); // 좌우 대칭 쌍으로 입력
t2 = scan.nextInt(); // 좌우 대칭 쌍으로 입력
ad.get(t1).add(t2); // 양방향 그래프이므로, vertex 1, 2 값 초기화
ad.get(t2).add(t1);
}
}
}
인접 행렬 vs 인접 리스트
두 가지 방식은 완전히 정반대의 특성을 가져서, 한 방식의 단점이 바로 다른 방식의 장점이기 때문에 그래프의 종류나 응용에 따라 적절히 사용해야 한다.
정점 u-v간의 간선 여부 확인
인접 행렬 - 정점 u, v가 주어졌을 때, 단 한 번의 배열의 접근만으로 연결 여부 파악 가능인접 리스트 - 인접 리스트를 처음부터 읽어나가면서 각 원소를 일일이 확인해야 함
공간 복잡도
인접 행렬 - V개의 Node를 표현하기 위해선 $V*V$ 개수 만큼의 공간이 필요하므로 공간 복잡도는 $O(V^2)$ 이다.
인접 리스트 - V개의 리스트에 실제 간선만큼 원소가 들어 있으므로 공간 복잡도는 $O(V+E)$ 이다.
만약 간선의 개수가 $V^2$ 에 수렴한다면 두 그래프 표현법의 공간 복잡도가 비슷할 수 있으나, 현실 세계에서는 간선의 수가 훨씬 적은 그래프가 많다.
간선의 수가 $V^2$에 비해 훨씬 적은 희소 그래프는 인접 리스트로 표현하고, 간선의 수가 $V^2$ 에 비례하는 밀접 그래프는 인접 행렬로 표현하는 것이 효율적이다.
2. 그래프 탐색알고리즘
이번 절에서는 그래프의 각 정점을 규칙적인 방법으로 순회하는 알고리즘인 그래프 탐색알고리즘에 대해 알아보자. 그래프 탐색알고리즘에는 DFS(깊이우선 탐색)과 BFS(너비우선탐색) 알고리즘이 있다.
DFS(깊이우선 탐색) : 재귀호출 가능
DFS는 "갈 수 있을 때까지 간다"는 전략을 간단하게 나타낸 것이다. 현재 정점에서 시작하여 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면 그 간선을 따라가는 방식이다. 만약 더 이상 갈 곳이 없어서 막힌 정점에 도달하면 포기하고, 마지막에 따라왔던 간선을 따라 뒤로 돌아가면서 탐색이 이루어진다.
DFS 진행과정

깊이우선 탐색은 지나간 정점을 계속해서 추적하기 위해 스택(재귀호출로 구현 시 내부적으로 자동 사용됨)을 사용한다 - 우선적으로 가장 낮은 인덱스부터 시작

정점 1을 방문한다. 스택에 최근 방문한 정점의 인덱스 1를 저장한다.(재귀호출로 구현 시 내부 스택에 정점 1이 자동 저장)
방문 정점 : 1
(내부) 스택 : 1
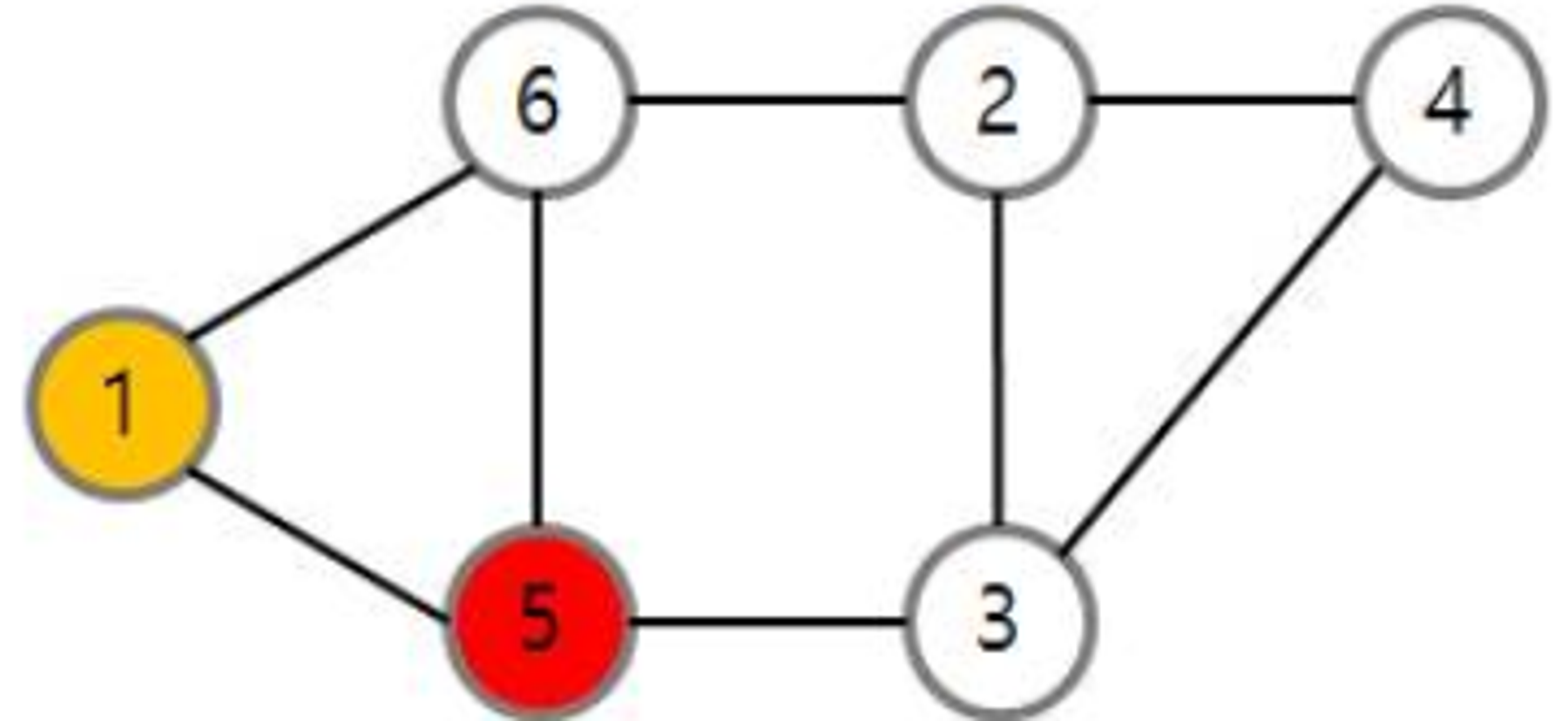
정점 1의 인접 정점 {5, 6} 중에서 인덱스가 작은 정점 5를 선택하여 방문한다.
방문 정점 : 1, 5
(내부) 스택 : 1, 5

정점 5의 미방문 인접 정점 {3, 6} 중에서 정점 3을 선택하여 방문한다.
방문 정점 : 1, 5, 3
(내부) 스택 : 1, 5, 3

정점 3의 미방문 인접 정점 {2, 4} 중에서 정점 2을 선택하여 방문한다.
방문 정점 : 1, 5, 3, 2
(내부) 스택 : 1, 5, 3, 2

정점 2의 미방문 인접 정점 {4, 6} 중에서 정점 4을 선택하여 방문한다.
방문 정점 : 1, 5, 3, 2, 4
(내부) 스택 : 1, 5, 3, 2, 4

정점 4와 연결된 정점을 찾아보니, 방문하지 않은 정점이 하나도 없다. 이 때 스택에서 정점 4를 꺼내고 정점 2로 돌아간다.
방문 정점 : 1, 5, 3, 2, 4
(내부) 스택 : 1, 5, 3, 2

같은 방식으로, 정점 2에 연결된 정점 중, 방문하지 않은 정점 6을 선택하여 방문한다. 그래프의 모든 정점을 방문하면, 알고리즘을 종료한다.
방문 정점 : 1, 5, 3, 2, 4, 6
(내부) 스택 : 1, 5, 3, 2, 6
방문 1 → 5 → 3 → 2 → 4 → 6

위의 그래프을 DFS 탐색 시 정점 방문 순서는?
A → B → E → B → F → C → F → B → A → D
=> A - B - E - F - C - D
깊이우선 탐색(DFS)의 중요한 특성 중 하나는 더 이상 따라갈 간선이 없을 경우 이전으로 돌아가야 한다는 점이다. 이를 구현하기 위해서는 지금까지 거쳐 온 정점들을 모두 저장해 둬야 하는데, 재귀 호출을 이용하면 시스템 내부적으로 스택이 자동으로 만들어져 사용된다.
다음은 깊이우선 탐색을 재귀 호출로 표현한 알고리즘이다.
입력 : 그래프 $G = (V, E)$, v는 탐색 시작정점
결과 : 깊이우선 탐색 순으로 각 정점 출력
dfs(v)
v를 방문되었다고 표시;
for all u∈ (v에 인접한 정점) do
if (u가 아직 방문되지 않았으면) then dfs(u)
다음은 인접 행렬로 표현된 무방향 그래프를 깊이우선 알고리즘으로 탐색하는 예제
public class DFSTest1 {
static int nE;
static int nV;
static int[][] ad;
static boolean[] visit; // 방문 여부 체크
public static void dfs(int i){
visit[i] = true; // 함수 호출 시, visit 했음을 표시
System.out.print(i+ " ");
for(int j = 1; j < nV+1; j++){
if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문
dfs(j);
}
}
}
public static void main(String[] args) {
nV = 6;
ad = new int[nV+1][nV+1]; // 변수 초기화
visit = new boolean[nV+1]; // 변수 초기화
// 인접 행렬로 그래프 표현(입력)
ad[1][5] = ad[5][1] = 1; // 간선들
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[2][4] = ad[4][2] = 1;
ad[2][6] = ad[6][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][5] = ad[5][3] = 1;
ad[5][6] = ad[6][5] = 1;
System.out.print("DFS : ");
dfs(1); // 1번부터 탐색 시작
}
}
다음은 인접 리스트로 표현된 무방향 그래프를 깊이 우선 알고리즘을 탐색하는 예제
BFS(너비우선 탐색) - 반복문만 사용 가능
BFS에서는 그래프의 정점 탐색 시 현재 위치에 인접한 모든 정점을 방문한 다음, 인접 정점들의 인접 정점들을 방문한다. BFS를 효과적으로 구현하기 위해 큐 자료구조가 사용된다.
BFS 진행 과정

위 그래프를 정점 1에서부터 너비우선 탐색 방법으로 탐색해 보자.

최초에 방문할 노드를 큐에 삽입한다.
방문 정점 : 1
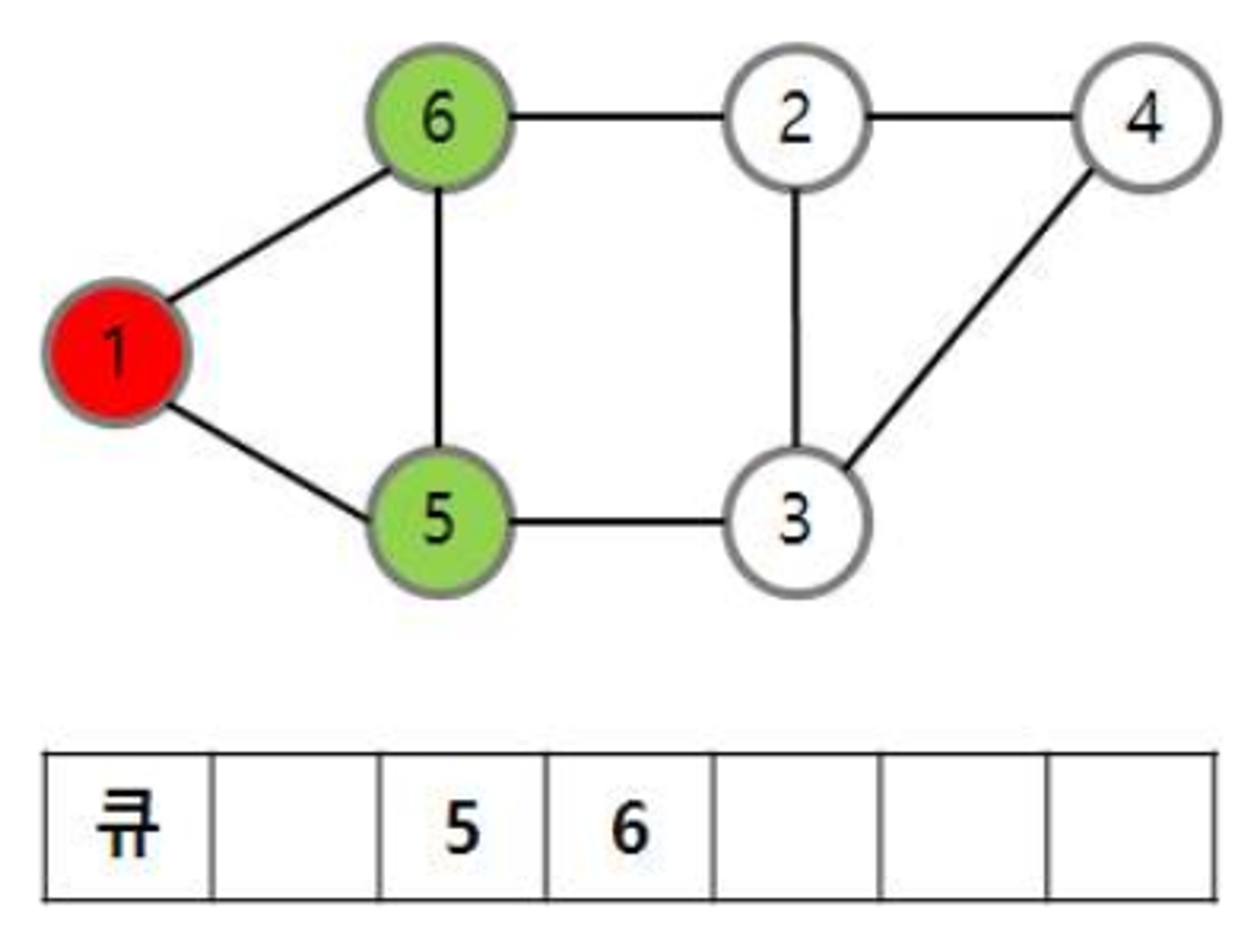
방문할 최초 노드의 값을 큐에서 꺼내고, 큐와 인접해 있는 정점 5, 6을 큐에 삽입한다.
방문 정점 : 1, 5, 6
출력 : 1

방문할 정점 5를 큐에서 꺼내고, 인접해 있는 정점들을 큐에 삽입한다. 여기서 정점 6은 기존에 큐에 있으므로 해당 데이터는 중복해서 넣지 않는다. 해시 테이블로 구현을 하든, visit 값을 미리 체크하던 큐에 입력할 데이터는 중복이 없어야 한다.
방문 정점 : 1, 5, 6, 3
출력 : 1->5

방문할 정점 6을 큐에서 꺼내고, 인접한 신규 정점 2를 큐에 삽입한다.
방문 정점 : 1, 5, 6, 3, 2
출력 : 1->5->6

방문할 정점 3을 큐에서 꺼내고, 인접한 정점 4를 큐에 삽입한다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3

방문할 정점 2를 큐에서 꺼낸다. 인접한 정점 4는 이미 방문했으므로 큐에 추가하지 않는다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3->2

방문할 정점 4을 큐에서 꺼낸다. 방문하지 않은 인접한 정점이 없으므로, 이 단계에서는 큐에 입력할 데이터가 없다. 큐가 비어있으면, 알고리즘을 멈춘다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3->2->4
BFS는 트리 구조의 레벨 오더와 같은 방식이다
다음은 너비우선 탐색을 큐를 이용하여 구현한 알고리즘
입력 : 그래프 $G=(V,E)$, v는 탐색 시작정점
결과 : 너비우선 탐색 순으로 각 정점 출력
bfs(v)
v를 방문되었다고 표시:
큐 Q에 정점 v를 삽입:
while (not is_empty(Q)) do
Q에서 정점 w를 삭제:
for all u∈ (w에 인접한 정점)do
if (u가 아직 방문되지 않았으면) then
u를 큐에 삽입;
u를 방문되었다고 표시:
간선이 있는데 방문이 안되어있으면 큐에 넣고 방문 true
다음은 인접 행렬로 표현된 그래프에서 BFS를 구현한 예제
자바 LinkedList 클래스를 사용하여 큐를 활용한다.
import java.util.*;
public class BFSTest1 {
static int[][] ad; // 인접 행렬
static boolean[] visit; // 방문체크 배열
static int Nv = 6;
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>(); // 큐 생성
q.offer(i);
visit[i] = true;
while (!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp+" ");
for (int j = 1; j <= Nv; j++)
if (ad[temp][j] == 1 && visit[j] == false) {
q.offer(j);
// 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력
visit[j] = true;
}
}
}
public static void main(String[] args){
ad = new int[Nv+1][Nv+1];
visit = new boolean[Nv+1];
// 인접 행렬로 그래프 표현(입력)
ad[1][5] = ad[5][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[2][4] = ad[4][2] = 1;
ad[2][6] = ad[6][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][5] = ad[5][3] = 1;
ad[5][6] = ad[6][5] = 1;
System.out.print("BFS : ");
bfs(1);
}
}
예제문제

4번 BFS(너비우선탐색) 결과 : A B C D E F
-
더보기
코드
package s240514; import java.util.*; public class BFS추가실습4 { static int[][] ad; // 인접 행렬 static boolean[] visit; // 방문체크 배열 static int Nv = 6; static char[] Vertexs; public static void bfs(int i) { Queue<Integer> q = new LinkedList<>(); // 큐 생성 q.offer(i); visit[i] = true; while (!q.isEmpty()) { int temp = q.poll(); System.out.print(Vertexs[temp]+" "); for (int j = 1; j <= Nv; j++) if (ad[temp][j] == 1 && visit[j] == false) { q.offer(j); // 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력 visit[j] = true; } } } public static void main(String[] args){ ad = new int[Nv+1][Nv+1]; visit = new boolean[Nv+1]; // 인접 행렬로 그래프 표현(입력) Vertexs = new char[]{' ','A', 'B', 'C', 'D', 'E', 'F'}; ad[1][2] = ad[2][1] = 1; // 간선들 ad[1][3] = ad[3][1] = 1; ad[1][4] = ad[4][1] = 1; ad[2][5] = ad[5][2] = 1; ad[2][6] = ad[6][2] = 1; ad[3][6] = ad[6][3] = 1; System.out.print("BFS : "); bfs(1); } }
4번 DFS(깊이우선탐색) 결과 : A B E F C D
-
더보기
package s240514; public class DFS추가실습4 { static int nE; // Edge 간선 static int nV; // Vertex 정점 static int[][] ad; // 인접 행렬 배열 static boolean[] visit; // 방문 여부 체크 static char[] adValue; public static void dfs(int i){ visit[i] = true; // 함수 호출 시, visit 했음을 표시 System.out.print(adValue[i]+ " "); for(int j = 1; j < nV+1; j++){ if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문 dfs(j); } } } public static void main(String[] args) { nV = 6; ad = new int[nV+1][nV+1]; // 변수 초기화 visit = new boolean[nV+1]; // 변수 초기화 // 인접 행렬로 그래프 표현(입력) adValue = new char[]{' ','A', 'B', 'C', 'D', 'E', 'F'}; ad[1][2] = ad[2][1] = 1; // 간선들 ad[1][3] = ad[3][1] = 1; ad[1][4] = ad[4][1] = 1; ad[2][5] = ad[5][2] = 1; ad[2][6] = ad[6][2] = 1; ad[3][6] = ad[6][3] = 1; System.out.print("DFS : "); dfs(1); // 1번부터 탐색 시작 } }
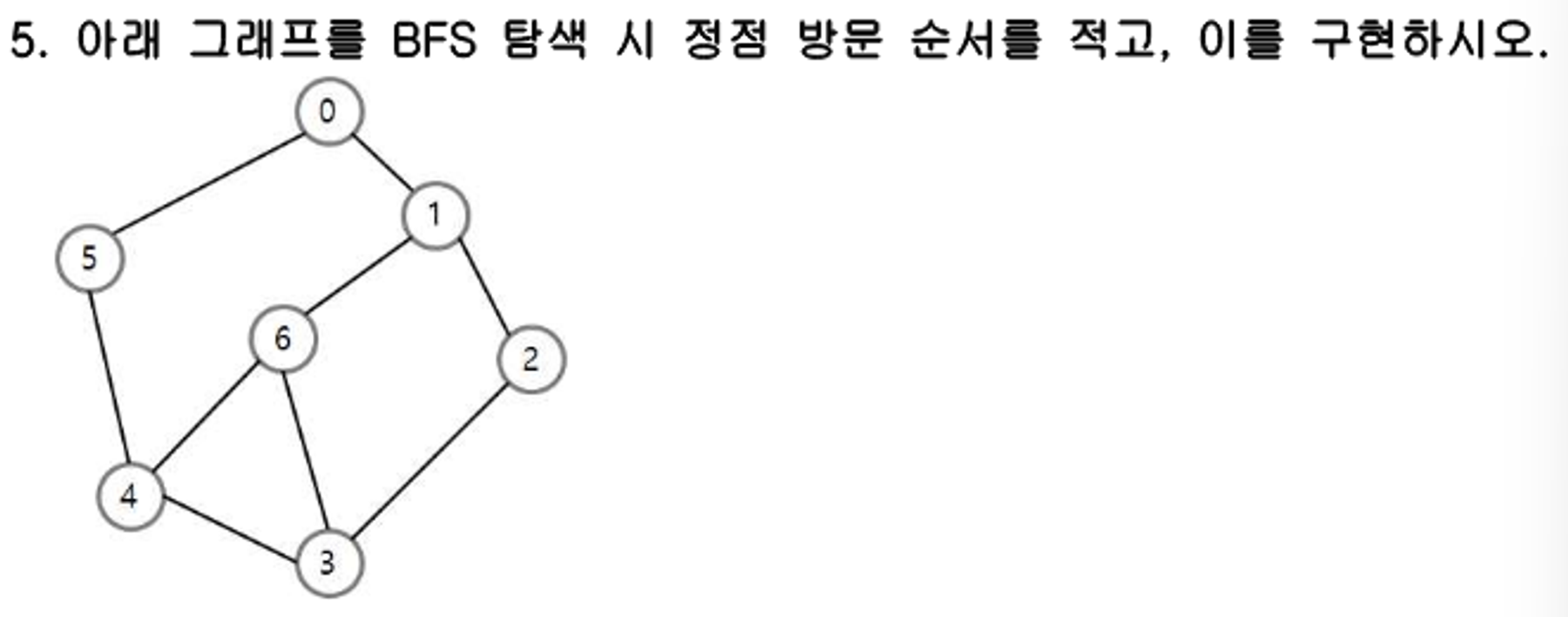
5번 BFS(너비우선탐색) 결과 : 0 1 5 2 6 4 3
package s240514;
import java.util.*;
public class BFS추가실습5 {
static int[][] ad; // 인접 행렬
static boolean[] visit; // 방문체크 배열
static int Nv = 7;
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>(); // 큐 생성
q.offer(i);
visit[i] = true;
while (!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp+" ");
for (int j = 0; j < Nv; j++)
if (ad[temp][j] == 1 && visit[j] == false) {
q.offer(j);
// 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력
visit[j] = true;
}
}
}
public static void main(String[] args){
ad = new int[Nv][Nv];
visit = new boolean[Nv];
// 인접 행렬로 그래프 표현(입력)
ad[0][1] = ad[1][0] = 1;
ad[0][5] = ad[5][0] = 1;
ad[1][2] = ad[2][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][6] = ad[6][3] = 1;
ad[4][5] = ad[5][4] = 1;
ad[4][6] = ad[6][4] = 1;
System.out.print("BFS : ");
bfs(0);
}
}5번 DFS(깊이우선탐색) 결과 : 0 1 2 3 4 5 6
package s240514;
public class DFS추가실습5 {
static int nE; // Edge 간선
static int nV; // Vertex 정점
static int[][] ad; // 인접 행렬 배열
static boolean[] visit; // 방문 여부 체크
public static void dfs(int i){
visit[i] = true; // 함수 호출 시, visit 했음을 표시
System.out.print(i+ " ");
for(int j = 0; j < nV; j++){
if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문
dfs(j);
}
}
}
public static void main(String[] args) {
nV = 7;
ad = new int[nV][nV]; // 변수 초기화
visit = new boolean[nV]; // 변수 초기화
// 인접 행렬로 그래프 표현(입력)
ad[0][1] = ad[1][0] = 1;
ad[0][5] = ad[5][0] = 1;
ad[1][2] = ad[2][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][6] = ad[6][3] = 1;
ad[4][5] = ad[5][4] = 1;
ad[4][6] = ad[6][4] = 1;
System.out.print("DFS : ");
dfs(0); // 0번부터 탐색 시작
}
}학습목표
- 정점, 간선, 경로, 차수 등 그래프 관련 용어를 이해한다.
- 인접 행렬, 인접 리스트로 그래프를 표현할 수 있다.
- DFS 알고리즘을 이해하고, 구현할 수 있다.
- BFS 알고리즘을 이해하고, 구현할 수 있다.
1. 그래프 개념
그래프 정의
그래프는 현실 세계의 다양한 관계를 표현하는 자료구조로, 여러 개의 노드(node) 또는 정점(vertex)이 간선(edge)으로 연결되어 있는 구조이다. 도로망, 지인 관계, 링크 관계, 프로세스와 자원 간의 관계 등을 그래프로 모델링할 수 있어 다양한 분야에서 활용된다. 그래프는 방향성과 순환성에 따라 다양한 종류의 그래프로 나뉘며, 이를 통해 다양한 문제들을 해결할 수 있다.
그래프 구성요소
그래프는 정점(Node, Vertex)과 간선(Edge) 들의 집합으로 구성된다. 간선은 정점간의 관계 나타내며 비용, 거리 등 가중치 값을 가질 수 있다.

위 그래프 G=(V, E)의 구성요소는 다음과 같다.
(V는 정점 집합, E는 간선집합)
V = {0, 1, 2, 3, 4, 5, 6}
E = {(0,1), (0,5), (1,2), (1,6), (2,3), (3,4), (3,6), (4,5), (4,6)}
도시 : 정점
도로끼리를 잇는 도로 : 간선
가중치는 있을 수도 있고 없을 수도 있음
배열표현법 → 2차원(인접 행렬, 인접 리스트)
그래프의 종류

가중치 그래프는 간선에 가중치가 있는 그래프이다. 정점 이동 간에 드는 비용이나, 거리등을 가중치로 표현한다.

그래프 경로(Path)와 사이클(Cycle)
경로란 연결 가능한 간선들의 순서 열이다. 아래의 그래프에서 (1, 2, 4, 5)는 정점 1에서 정점 5로 가는 경로가 맞지만, (1, 2, 3)은 간선 <2, 3>이 없으므로 경로가 아니다.

사이클은 같은 정점으로 되돌아오는 경로이다.
위 그래프에서 (1, 2, 4, 3, 1)은 정점 1에서 출발해서, 정점 1로 되돌아 오기 때문에 사이클이다.
만약 6을 방문하고 싶을때 순서는 1 → 2 → 4 → 3 → 1 → 이런식으로 무한루프가 발생할 수 도 있음
그래프에서는 사이클을 체크하는것, 피해가는게 굉장히 중요하다.
그래프의 표현
그래프 자료구조를 메모리에 표현하는 방법은 다른 자료구조와 마찬가지로 배열을 이용하는 방법(인접 행렬)과 연결리스트를 이용하는 방법(인접 리스트)이 있다.
인접 행렬(Adjacent Matrix)

간선이 있으면 1, 없으면 0 → 그래서 2차원이 될 수 밖에 없음
무방향 그래프를 인접 행렬로 표현하는 예제
import java.util.Scanner;
// 무방향 그래프를 인접 행렬로 표현
public class GraphTest1 {
static int nE;
static int nV;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nV = scan.nextInt(); // Vertex (정점)
nE = scan.nextInt(); // Edge (간선)
// Vertex의 이름을 그대로 사용하기 위해 (nV+1)(nV+1)개만큼 배열 생성
int[][] ad = new int[nV+1][nV+1];
for(int i = 0; i < nE; i++){ // Edge 정보 입력 받음
int t1 = scan.nextInt();
int t2 = scan.nextInt();
ad[t1][t2] = ad[t2][t1] = 1; // 1대신 가중치를 넣으면 가중치 그래프
}
}
}
인접 리스트(Adjacent List)
그래프를 표현하는 두 번째 방법은 연결리스트를 이용하는 방법이다. 이를, 인접 리스트라한다.
인접 리스트 방식에서는 정점의 수만큼 연결리스트를 생성하고, 각 정점 연결리스트에 연결된 정점을 추가한다
무방향 그래프를 인접 리스트로 표현한 그림

리스트 개수가 정점 개수만큼 생긴다.
그래프의 각 정점마다 해당 정점에서 나가는 간선의 목록을 저장하기위해 각 정점마다 하나의 연결리스트를 갖는 방식으로 구현한다.
무방향 그래프를 인접 리스트로 표현하는 예제
public class GraphTest2 {
static int nV; // 총 vertex 개수
static int nE; // 총 edge 개
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nV = scan.nextInt();
nE = scan.nextInt();
// 인접 리스트 초기화
ArrayList<ArrayList<Integer>> ad = new ArrayList<>();
for(int i = 0; i < nV; i++) { // 정점 개수만큼 ArrayList 생성
ad.add(new<Integer> ArrayList()); // ad 리스트에 담을 리스트 초기화
}
for(int i = 0; i < nE; i++) {
int t1, t2; // vertex 두 개 입력 받기
t1 = scan.nextInt(); // 좌우 대칭 쌍으로 입력
t2 = scan.nextInt(); // 좌우 대칭 쌍으로 입력
ad.get(t1).add(t2); // 양방향 그래프이므로, vertex 1, 2 값 초기화
ad.get(t2).add(t1);
}
}
}
인접 행렬 vs 인접 리스트
두 가지 방식은 완전히 정반대의 특성을 가져서, 한 방식의 단점이 바로 다른 방식의 장점이기 때문에 그래프의 종류나 응용에 따라 적절히 사용해야 한다.
정점 u-v간의 간선 여부 확인
인접 행렬 - 정점 u, v가 주어졌을 때, 단 한 번의 배열의 접근만으로 연결 여부 파악 가능인접 리스트 - 인접 리스트를 처음부터 읽어나가면서 각 원소를 일일이 확인해야 함
공간 복잡도
인접 행렬 - V개의 Node를 표현하기 위해선 개수 만큼의 공간이 필요하므로 공간 복잡도는 이다.
인접 리스트 - V개의 리스트에 실제 간선만큼 원소가 들어 있으므로 공간 복잡도는 이다.
만약 간선의 개수가 에 수렴한다면 두 그래프 표현법의 공간 복잡도가 비슷할 수 있으나, 현실 세계에서는 간선의 수가 훨씬 적은 그래프가 많다.
간선의 수가 에 비해 훨씬 적은 희소 그래프는 인접 리스트로 표현하고, 간선의 수가 에 비례하는 밀접 그래프는 인접 행렬로 표현하는 것이 효율적이다.
2. 그래프 탐색알고리즘
이번 절에서는 그래프의 각 정점을 규칙적인 방법으로 순회하는 알고리즘인 그래프 탐색알고리즘에 대해 알아보자. 그래프 탐색알고리즘에는 DFS(깊이우선 탐색)과 BFS(너비우선탐색) 알고리즘이 있다.
DFS(깊이우선 탐색) : 재귀호출 가능
DFS는 "갈 수 있을 때까지 간다"는 전략을 간단하게 나타낸 것이다. 현재 정점에서 시작하여 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면 그 간선을 따라가는 방식이다. 만약 더 이상 갈 곳이 없어서 막힌 정점에 도달하면 포기하고, 마지막에 따라왔던 간선을 따라 뒤로 돌아가면서 탐색이 이루어진다.
DFS 진행과정

깊이우선 탐색은 지나간 정점을 계속해서 추적하기 위해 스택(재귀호출로 구현 시 내부적으로 자동 사용됨)을 사용한다 - 우선적으로 가장 낮은 인덱스부터 시작

정점 1을 방문한다. 스택에 최근 방문한 정점의 인덱스 1를 저장한다.(재귀호출로 구현 시 내부 스택에 정점 1이 자동 저장)
방문 정점 : 1
(내부) 스택 : 1

정점 1의 인접 정점 {5, 6} 중에서 인덱스가 작은 정점 5를 선택하여 방문한다.
방문 정점 : 1, 5
(내부) 스택 : 1, 5

정점 5의 미방문 인접 정점 {3, 6} 중에서 정점 3을 선택하여 방문한다.
방문 정점 : 1, 5, 3
(내부) 스택 : 1, 5, 3

정점 3의 미방문 인접 정점 {2, 4} 중에서 정점 2을 선택하여 방문한다.
방문 정점 : 1, 5, 3, 2
(내부) 스택 : 1, 5, 3, 2

정점 2의 미방문 인접 정점 {4, 6} 중에서 정점 4을 선택하여 방문한다.
방문 정점 : 1, 5, 3, 2, 4
(내부) 스택 : 1, 5, 3, 2, 4

정점 4와 연결된 정점을 찾아보니, 방문하지 않은 정점이 하나도 없다. 이 때 스택에서 정점 4를 꺼내고 정점 2로 돌아간다.
방문 정점 : 1, 5, 3, 2, 4
(내부) 스택 : 1, 5, 3, 2

같은 방식으로, 정점 2에 연결된 정점 중, 방문하지 않은 정점 6을 선택하여 방문한다. 그래프의 모든 정점을 방문하면, 알고리즘을 종료한다.
방문 정점 : 1, 5, 3, 2, 4, 6
(내부) 스택 : 1, 5, 3, 2, 6
방문 1 → 5 → 3 → 2 → 4 → 6

위의 그래프을 DFS 탐색 시 정점 방문 순서는?
A → B → E → B → F → C → F → B → A → D
=> A - B - E - F - C - D
깊이우선 탐색(DFS)의 중요한 특성 중 하나는 더 이상 따라갈 간선이 없을 경우 이전으로 돌아가야 한다는 점이다. 이를 구현하기 위해서는 지금까지 거쳐 온 정점들을 모두 저장해 둬야 하는데, 재귀 호출을 이용하면 시스템 내부적으로 스택이 자동으로 만들어져 사용된다.
다음은 깊이우선 탐색을 재귀 호출로 표현한 알고리즘이다.
입력 : 그래프 , v는 탐색 시작정점
결과 : 깊이우선 탐색 순으로 각 정점 출력
dfs(v)
v를 방문되었다고 표시;
for all u∈ (v에 인접한 정점) do
if (u가 아직 방문되지 않았으면) then dfs(u)
다음은 인접 행렬로 표현된 무방향 그래프를 깊이우선 알고리즘으로 탐색하는 예제
public class DFSTest1 {
static int nE;
static int nV;
static int[][] ad;
static boolean[] visit; // 방문 여부 체크
public static void dfs(int i){
visit[i] = true; // 함수 호출 시, visit 했음을 표시
System.out.print(i+ " ");
for(int j = 1; j < nV+1; j++){
if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문
dfs(j);
}
}
}
public static void main(String[] args) {
nV = 6;
ad = new int[nV+1][nV+1]; // 변수 초기화
visit = new boolean[nV+1]; // 변수 초기화
// 인접 행렬로 그래프 표현(입력)
ad[1][5] = ad[5][1] = 1; // 간선들
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[2][4] = ad[4][2] = 1;
ad[2][6] = ad[6][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][5] = ad[5][3] = 1;
ad[5][6] = ad[6][5] = 1;
System.out.print("DFS : ");
dfs(1); // 1번부터 탐색 시작
}
}
다음은 인접 리스트로 표현된 무방향 그래프를 깊이 우선 알고리즘을 탐색하는 예제
BFS(너비우선 탐색) - 반복문만 사용 가능
BFS에서는 그래프의 정점 탐색 시 현재 위치에 인접한 모든 정점을 방문한 다음, 인접 정점들의 인접 정점들을 방문한다. BFS를 효과적으로 구현하기 위해 큐 자료구조가 사용된다.
BFS 진행 과정

위 그래프를 정점 1에서부터 너비우선 탐색 방법으로 탐색해 보자.

최초에 방문할 노드를 큐에 삽입한다.
방문 정점 : 1

방문할 최초 노드의 값을 큐에서 꺼내고, 큐와 인접해 있는 정점 5, 6을 큐에 삽입한다.
방문 정점 : 1, 5, 6
출력 : 1

방문할 정점 5를 큐에서 꺼내고, 인접해 있는 정점들을 큐에 삽입한다. 여기서 정점 6은 기존에 큐에 있으므로 해당 데이터는 중복해서 넣지 않는다. 해시 테이블로 구현을 하든, visit 값을 미리 체크하던 큐에 입력할 데이터는 중복이 없어야 한다.
방문 정점 : 1, 5, 6, 3
출력 : 1->5

방문할 정점 6을 큐에서 꺼내고, 인접한 신규 정점 2를 큐에 삽입한다.
방문 정점 : 1, 5, 6, 3, 2
출력 : 1->5->6

방문할 정점 3을 큐에서 꺼내고, 인접한 정점 4를 큐에 삽입한다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3

방문할 정점 2를 큐에서 꺼낸다. 인접한 정점 4는 이미 방문했으므로 큐에 추가하지 않는다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3->2

방문할 정점 4을 큐에서 꺼낸다. 방문하지 않은 인접한 정점이 없으므로, 이 단계에서는 큐에 입력할 데이터가 없다. 큐가 비어있으면, 알고리즘을 멈춘다.
방문 정점 : 1, 5, 6, 3, 2, 4
출력 : 1->5->6->3->2->4
BFS는 트리 구조의 레벨 오더와 같은 방식이다
다음은 너비우선 탐색을 큐를 이용하여 구현한 알고리즘
입력 : 그래프 , v는 탐색 시작정점
결과 : 너비우선 탐색 순으로 각 정점 출력
bfs(v)
v를 방문되었다고 표시:
큐 Q에 정점 v를 삽입:
while (not is_empty(Q)) do
Q에서 정점 w를 삭제:
for all u∈ (w에 인접한 정점)do
if (u가 아직 방문되지 않았으면) then
u를 큐에 삽입;
u를 방문되었다고 표시:
간선이 있는데 방문이 안되어있으면 큐에 넣고 방문 true
다음은 인접 행렬로 표현된 그래프에서 BFS를 구현한 예제
자바 LinkedList 클래스를 사용하여 큐를 활용한다.
import java.util.*;
public class BFSTest1 {
static int[][] ad; // 인접 행렬
static boolean[] visit; // 방문체크 배열
static int Nv = 6;
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>(); // 큐 생성
q.offer(i);
visit[i] = true;
while (!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp+" ");
for (int j = 1; j <= Nv; j++)
if (ad[temp][j] == 1 && visit[j] == false) {
q.offer(j);
// 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력
visit[j] = true;
}
}
}
public static void main(String[] args){
ad = new int[Nv+1][Nv+1];
visit = new boolean[Nv+1];
// 인접 행렬로 그래프 표현(입력)
ad[1][5] = ad[5][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[2][4] = ad[4][2] = 1;
ad[2][6] = ad[6][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][5] = ad[5][3] = 1;
ad[5][6] = ad[6][5] = 1;
System.out.print("BFS : ");
bfs(1);
}
}
예제문제

4번 BFS(너비우선탐색) 결과 : A B C D E F
-
더보기
코드
package s240514; import java.util.*; public class BFS추가실습4 { static int[][] ad; // 인접 행렬 static boolean[] visit; // 방문체크 배열 static int Nv = 6; static char[] Vertexs; public static void bfs(int i) { Queue<Integer> q = new LinkedList<>(); // 큐 생성 q.offer(i); visit[i] = true; while (!q.isEmpty()) { int temp = q.poll(); System.out.print(Vertexs[temp]+" "); for (int j = 1; j <= Nv; j++) if (ad[temp][j] == 1 && visit[j] == false) { q.offer(j); // 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력 visit[j] = true; } } } public static void main(String[] args){ ad = new int[Nv+1][Nv+1]; visit = new boolean[Nv+1]; // 인접 행렬로 그래프 표현(입력) Vertexs = new char[]{' ','A', 'B', 'C', 'D', 'E', 'F'}; ad[1][2] = ad[2][1] = 1; // 간선들 ad[1][3] = ad[3][1] = 1; ad[1][4] = ad[4][1] = 1; ad[2][5] = ad[5][2] = 1; ad[2][6] = ad[6][2] = 1; ad[3][6] = ad[6][3] = 1; System.out.print("BFS : "); bfs(1); } }
4번 DFS(깊이우선탐색) 결과 : A B E F C D
-
더보기
package s240514; public class DFS추가실습4 { static int nE; // Edge 간선 static int nV; // Vertex 정점 static int[][] ad; // 인접 행렬 배열 static boolean[] visit; // 방문 여부 체크 static char[] adValue; public static void dfs(int i){ visit[i] = true; // 함수 호출 시, visit 했음을 표시 System.out.print(adValue[i]+ " "); for(int j = 1; j < nV+1; j++){ if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문 dfs(j); } } } public static void main(String[] args) { nV = 6; ad = new int[nV+1][nV+1]; // 변수 초기화 visit = new boolean[nV+1]; // 변수 초기화 // 인접 행렬로 그래프 표현(입력) adValue = new char[]{' ','A', 'B', 'C', 'D', 'E', 'F'}; ad[1][2] = ad[2][1] = 1; // 간선들 ad[1][3] = ad[3][1] = 1; ad[1][4] = ad[4][1] = 1; ad[2][5] = ad[5][2] = 1; ad[2][6] = ad[6][2] = 1; ad[3][6] = ad[6][3] = 1; System.out.print("DFS : "); dfs(1); // 1번부터 탐색 시작 } }

5번 BFS(너비우선탐색) 결과 : 0 1 5 2 6 4 3
package s240514;
import java.util.*;
public class BFS추가실습5 {
static int[][] ad; // 인접 행렬
static boolean[] visit; // 방문체크 배열
static int Nv = 7;
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>(); // 큐 생성
q.offer(i);
visit[i] = true;
while (!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp+" ");
for (int j = 0; j < Nv; j++)
if (ad[temp][j] == 1 && visit[j] == false) {
q.offer(j);
// 큐에 넣을 노드들을 잠재적으로 방문한다는 가정하에 입력
visit[j] = true;
}
}
}
public static void main(String[] args){
ad = new int[Nv][Nv];
visit = new boolean[Nv];
// 인접 행렬로 그래프 표현(입력)
ad[0][1] = ad[1][0] = 1;
ad[0][5] = ad[5][0] = 1;
ad[1][2] = ad[2][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][6] = ad[6][3] = 1;
ad[4][5] = ad[5][4] = 1;
ad[4][6] = ad[6][4] = 1;
System.out.print("BFS : ");
bfs(0);
}
}5번 DFS(깊이우선탐색) 결과 : 0 1 2 3 4 5 6
package s240514;
public class DFS추가실습5 {
static int nE; // Edge 간선
static int nV; // Vertex 정점
static int[][] ad; // 인접 행렬 배열
static boolean[] visit; // 방문 여부 체크
public static void dfs(int i){
visit[i] = true; // 함수 호출 시, visit 했음을 표시
System.out.print(i+ " ");
for(int j = 0; j < nV; j++){
if(ad[i][j] == 1 && visit[j] == false){ // j를 방문하지 않았으면 j를 방문
dfs(j);
}
}
}
public static void main(String[] args) {
nV = 7;
ad = new int[nV][nV]; // 변수 초기화
visit = new boolean[nV]; // 변수 초기화
// 인접 행렬로 그래프 표현(입력)
ad[0][1] = ad[1][0] = 1;
ad[0][5] = ad[5][0] = 1;
ad[1][2] = ad[2][1] = 1;
ad[1][6] = ad[6][1] = 1;
ad[2][3] = ad[3][2] = 1;
ad[3][4] = ad[4][3] = 1;
ad[3][6] = ad[6][3] = 1;
ad[4][5] = ad[5][4] = 1;
ad[4][6] = ad[6][4] = 1;
System.out.print("DFS : ");
dfs(0); // 0번부터 탐색 시작
}
}